The Multivariable Alexander Polynomial: Difference between revisions
DrorsRobot (talk | contribs) No edit summary |
No edit summary |
||
| Line 58: | Line 58: | ||
<!--END--> |
<!--END--> |
||
But notice the funny labelling of the components! |
But notice the funny labelling of the components! The program <code>MultivariableAlexander</code> orders the variables in its output (typically denoted <code>t[i]</code>) in the same order as the order of the components of a link <code>L</code> as they appear within <code>Skeleton[L]</code>. Hence we had to rename <code>t[3]</code> to be <code>t4</code> and <code>t[4]</code> to be <code>t3</code>. |
||
(To be precise, <code>MultivariableAlexander</code> orders the components so that its output would be lexicographically minimal among all possible orderings. This way it is at least guaranteed that different presentations for the same link will yield the same output for <code>MultivariableAlexander</code>.) |
|||
====Links with Vanishing Multivariable Alexander Polynomial==== |
====Links with Vanishing Multivariable Alexander Polynomial==== |
||
| Line 119: | Line 117: | ||
<!--END--> |
<!--END--> |
||
We don't know whether our mystery link appears in the link table as is, or as a mirror, or with its two components switched. Hence we let < |
We don't know whether our mystery link appears in the link table as is, or as a mirror, or with its two components switched. Hence we let <code>AllPossibilities</code> contain the multivariable Alexander polynomials of all those possibilities: |
||
<!--$$AllPossibilities = Union[Flatten[ |
<!--$$AllPossibilities = Union[Flatten[ |
||
Revision as of 10:51, 28 April 2009
(For In[1] see Setup)
|
| ||||||||
 L8a21 |
The link L8a21 is symmetric under cyclic permutations of its components but not under interchanging two adjacent components. It is amusing to see how this is reflected in its multivariable Alexander polynomial:
In[3]:=
|
mva = MultivariableAlexander[Link[8, Alternating, 21]][t] /. {
t[1] -> t1, t[2] -> t2, t[3] -> t4, t[4] -> t3
}
|
Out[3]=
|
(-t1 - t2 + t1 t2 - t3 + 2 t1 t3 + t2 t3 - t1 t2 t3 - t4 + t1 t4 +
2 t2 t4 - t1 t2 t4 + t3 t4 - t1 t3 t4 - t2 t3 t4) /
(Sqrt[t1] Sqrt[t2] Sqrt[t3] Sqrt[t4])
|
In[4]:=
|
mva - (mva /. {t1->t2, t2->t3, t3->t4, t4->t1})
|
Out[4]=
|
0
|
In[5]:=
|
Simplify[mva - (mva /. {t1->t2, t2->t1})]
|
Out[5]=
|
(t1 - t2) (t3 - t4)
-----------------------------------
Sqrt[t1] Sqrt[t2] Sqrt[t3] Sqrt[t4]
|
But notice the funny labelling of the components! The program MultivariableAlexander orders the variables in its output (typically denoted t[i]) in the same order as the order of the components of a link L as they appear within Skeleton[L]. Hence we had to rename t[3] to be t4 and t[4] to be t3.
Links with Vanishing Multivariable Alexander Polynomial
There are 11 links with up to 11 crossings whose multivariable Alexander polynomial is [math]\displaystyle{ 0 }[/math]. Here they are:
In[6]:=
|
Select[AllLinks[], (MultivariableAlexander[#][t] == 0) &]
|
Out[6]=
|
{Link[9, NonAlternating, 27], Link[10, NonAlternating, 32],
Link[10, NonAlternating, 36], Link[10, NonAlternating, 107],
Link[11, NonAlternating, 244], Link[11, NonAlternating, 247],
Link[11, NonAlternating, 334], Link[11, NonAlternating, 381],
Link[11, NonAlternating, 396], Link[11, NonAlternating, 404],
Link[11, NonAlternating, 406]}
|
 L9n27 |
 L10n32 |
 L10n36 |
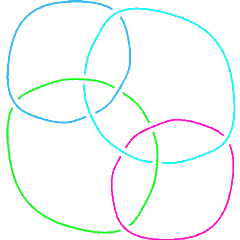 L10n107 |
 L11n244 |
 L11n247 |
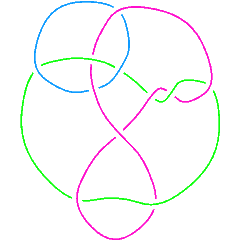 L11n334 |
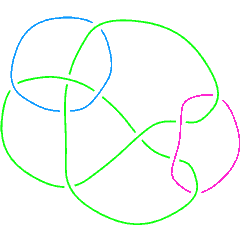 L11n381 |
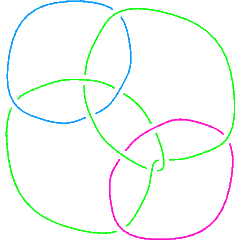 L11n396 |
 L11n404 |
 L11n406 |
Dror doesn't understand the multivariable Alexander polynomial well enough to give simple topological reasons for the vanishing of the said polynomial for these knots. (Though see the Talk Page).
Detecting a Link Using the Multivariable Alexander Polynomial
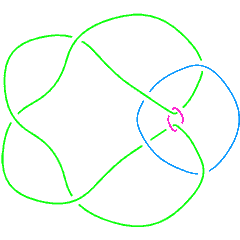
On May 1, 2007 AnonMoos asked Dror if he could identify the link in the figure on the right. So Dror typed:
In[7]:=
|
mva = MultivariableAlexander[L = PD[
X[1, 16, 2, 17], X[3, 15, 4, 14], X[5, 8, 6, 9],
X[7, 21, 8, 20], X[9, 22, 10, 13], X[11, 2, 12, 3],
X[13, 18, 14, 19], X[15, 12, 16, 1], X[17, 11, 18, 10],
X[19, 4, 20, 5], X[21, 7, 22, 6]
]][t]
|
Out[7]=
|
2
-(((-1 + t[1]) (-1 + t[2]) (1 - 2 t[1] + t[1] - 2 t[2] + 2 t[1] t[2] -
2 2 2 2 2
2 t[1] t[2] + t[2] - 2 t[1] t[2] + t[1] t[2] )) /
3/2 3/2
(t[1] t[2] ))
|
We don't know whether our mystery link appears in the link table as is, or as a mirror, or with its two components switched. Hence we let AllPossibilities contain the multivariable Alexander polynomials of all those possibilities:
In[8]:=
|
AllPossibilities = Union[Flatten[
{mva, -mva} /. {{}, {t[1] -> t[2], t[2] -> t[1]}}
]]
|
Out[8]=
|
2
{-(((-1 + t[1]) (-1 + t[2]) (1 - 2 t[1] + t[1] - 2 t[2] +
2 2 2 2 2
2 t[1] t[2] - 2 t[1] t[2] + t[2] - 2 t[1] t[2] + t[1] t[2]
3/2 3/2
)) / (t[1] t[2] )),
2
((-1 + t[1]) (-1 + t[2]) (1 - 2 t[1] + t[1] - 2 t[2] + 2 t[1] t[2] -
2 2 2 2 2
2 t[1] t[2] + t[2] - 2 t[1] t[2] + t[1] t[2] )) /
3/2 3/2
(t[1] t[2] )}
|
Finally, let us locate our link in the link table:
In[9]:=
|
Select[
AllLinks[],
MemberQ[AllPossibilities, MultivariableAlexander[#][t]] &
]
|
Out[9]=
|
{Link[11, Alternating, 289]}
|
And just to be sure,
In[10]:=
|
{Jones[L][q], Jones[Link[11, Alternating, 289]][q]}
|
Out[10]=
|
-(17/2) 4 8 12 16 18 17 15
{q - ----- + ----- - ----- + ---- - ---- + ---- - ---- +
15/2 13/2 11/2 9/2 7/2 5/2 3/2
q q q q q q q
10 3/2 5/2
------- - 7 Sqrt[q] + 3 q - q ,
Sqrt[q]
-(5/2) 3 7 3/2 5/2
-q + ---- - ------- + 10 Sqrt[q] - 15 q + 17 q -
3/2 Sqrt[q]
q
7/2 9/2 11/2 13/2 15/2 17/2
18 q + 16 q - 12 q + 8 q - 4 q + q }
|
Thus the mystery link is the mirror image of L11a289.
