The Determinant and the Signature

KnotTheory`/Navigation  The Mathematica Package KnotTheory` Acknowledgement Setup Naming and Enumeration Presentations Planar Diagrams Some further details Gauss Codes DT (Dowker-Thistlethwaite) Codes Braid Representatives MorseLink Presentations Arc Presentations Conway Notation Graphical Input Graphical Output Drawing Planar Diagrams How does it work? Drawing MorseLink Presentations Drawing Braids Structure and Operations Invariants Invariants from Braid Theory Three Dimensional Invariants The Alexander-Conway Polynomial The Multivariable Alexander Polynomial The Determinant and the Signature The Jones Polynomial How is the Jones polynomial computed? The Coloured Jones Polynomials The A2 Invariant Quantum knot invariants The HOMFLY-PT Polynomial The Kauffman Polynomial Finite Type (Vassiliev) Invariants Khovanov Homology Heegaard Floer Knot Homology R-Matrix Invariants Extras Included with KnotTheory` Drawing with TubePlot Standalone_TubePlot Using the LinKnot package WikiLink QuantumGroups` Lightly Documented Features A Sample KnotTheory` Session Further Usage Example Prime Links with a Non-Prime Component "Rubberband" Brunnian Links Identifying Knots within a List Cabling Burau's Theorem Further Knot Theory Software KnotPlot Knotscape Xknots Extending/Modifying KnotTheory` Bugs How to Edit this Manual...

(For In[1] see Setup)

In[1]:= ?KnotDet KnotDet[K] returns the determinant of a knot K.

In[2]:= ?KnotSignature KnotSignature[K] returns the signature of a knot K.

Thus, for example, the knots 5_1 and 10_132 have the same determinant (and even the same Alexander and Jones polynomials), but different signatures:

5_1

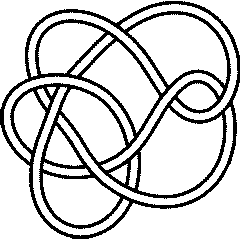10_132

In[3]:=	KnotDet /@ {Knot[5, 1], Knot[10, 132]}
Out[3]=	{5, 5}

In[4]:=	{ Equal @@ (Jones[#][q]& /@ {Knot[5, 1], Knot[10, 132]}), Equal @@ (Alexander[#][t]& /@ {Knot[5, 1], Knot[10, 132]}) }
Out[4]=	{True, True}

In[5]:=	KnotSignature /@ {Knot[5, 1], Knot[10, 132]}
Out[5]=	{-4, 0}

In August 2005 somebody emailed Dror a question about knot colouring, which amounted to "find the first knot (other than the unknot) whose determinant is $\pm 1$. So on September 2^nd Dror typed

In[6]:=	Select[AllKnots[], Abs[KnotDet[#]] == 1 &]
Out[6]=	{Knot[0, 1], Knot[10, 124], Knot[10, 153], Knot[11, NonAlternating, 34], Knot[11, NonAlternating, 42], Knot[11, NonAlternating, 49], Knot[11, NonAlternating, 116]}

Hence the first few knots that are not $k$-colourable for any $k$ are 10_124, 10_153, K11n34, K11n42, K11n49 and K11n116.

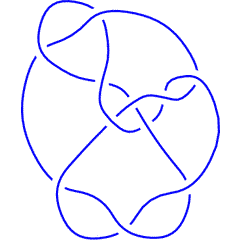K11n116