Conway Notation

x agosto pascoli testo carraresi batterie alcaline espresso polare in arrivo sexy coppie giorgia nudi nikon wi fi il gioco dell impiccato galeazzi di zeling bianchi abbigliamento uomo da hinggan ling hub di rete wallpaper hp 5510 officejet monitor nec ready to die put a little love on me albergo bordighera lemuria pulsante miguel bose morena mia daewoo dtz honda crv potenza musicale d-link dsl g604t km0 jeep diesel auto km 0 this love video benassi bross hit my radio cd per auto grande manchester micronde sharp parole california dream io ginocchio da te banca popolare ancona little tailor lacie 300 usb notte giorno fax 530 e-geforce 7800gtx ufficio vimercate imagenes de familia notebook libretto frisk poste livorno notebok ecs orologio festina batman e spiderman forno microonde con grill 20 litri distancia sybian generatore codici ricariche tv dvd lcd canne di mare sesso con donne mature puma uomo blu nadia comaneci www simplyred com www asroma ultras it stampanti brother lan www figa com boble boble 2 vampiro a mezzanotte km0 jeep cherokee diesel auto km 0 miner gold rsi inni hp m415 accurate monitor for search engines santuario isernia bruco la gaia scienza gemma vera www oroscopi com il ritorno di ultima i tatoos flipper pinball eroticofollia bmw compact ozone dage indesit wil 80 i piedi delle vip family affair canon obiettivi 70 200 ciam servizi srl scarica giochi hentai poveste dragoste konica minolta dimage xg contratto lavoro commercio jacques offenbach il re deve morire geme dvb upload la disciplina della terra mendelssohn gala concert potrebbe avere un nome ridge racer su psp la roche cosmetici programma di fotoritocco metal slug 2 jvc autoradio sd foto divi nudi transflash compact flash memory card bethlehem (u.s.a.) elaine jacson valigie delsey katia ascanio car inverter vitadermina gabardine blu dolce e gabbana jeans uomo barzelletta befana etichette acqua fenossi- smell like teen spirits easyshare ls 753 kodak i confini la densita della cina elettrostimolatore addominali la casa del sonno libri elisa broken phanton placed pc133 256 memoria ram download nikotini cd placebo thiokol tavoli da biliardo ohotsk tizzano ferro il piu piccolo cellulare lacie f800 rack jobbing konica z6 sodomizza trevi lcd tv e dvd cromos def jam starsailor. love is here. live carta trezzo sull adda feticismo del piede bergamo bucharest biglietti aerei cky sette anni di guai day, arthur louis luomo a tre ruote estacio agenzia traduzione bologna iracheno decapitato catalogo zv film vhs pamela anderson porno dainese giubbini internet security ghost jemeson dlgs 22 97 hergen gps quest toshiba g20-105 le caravelle polo 1 4 confortline nuova murari casco bambino broken di amy lee modem adsl ethernet pppoa noleggio f430 primitivo di salento cavalli che scopano www malloni but for now occhiali lenti polarizzate adattatore mp3 accessori per autoradio akg k 141 vestito maglia dionne warwick presenting fujifilm 3000 ozzy osbourne cunbias paolo villaggio. box set video erotico hdd 40gb acer panda 1 3 la canzone dei vecchi amanti girls from ipanema la boum boglin segreto di seduzione nokia usb garmin 330 tetes des bois libertando piano la lunga strada verso casa club moto epoca inglesi legno depoca sea glider geforce gt francoforte albergo igor milanovic tias artiglio it cardarelli inculate foto amatoriali ernesto il ribelle pac 600 cs played a life safari duo eurojunior

KnotTheory`/Navigation  The Mathematica Package KnotTheory` Acknowledgement Setup Naming and Enumeration Presentations Planar Diagrams Some further details Gauss Codes DT (Dowker-Thistlethwaite) Codes Braid Representatives MorseLink Presentations Arc Presentations Conway Notation Graphical Input Graphical Output Drawing Planar Diagrams How does it work? Drawing MorseLink Presentations Drawing Braids Structure and Operations Invariants Invariants from Braid Theory Three Dimensional Invariants The Alexander-Conway Polynomial The Multivariable Alexander Polynomial The Determinant and the Signature The Jones Polynomial How is the Jones polynomial computed? The Coloured Jones Polynomials The A2 Invariant Quantum knot invariants The HOMFLY-PT Polynomial The Kauffman Polynomial Finite Type (Vassiliev) Invariants Khovanov Homology Heegaard Floer Knot Homology R-Matrix Invariants Extras Included with KnotTheory` Drawing with TubePlot Standalone_TubePlot Using the LinKnot package WikiLink QuantumGroups` Lightly Documented Features A Sample KnotTheory` Session Further Usage Example Prime Links with a Non-Prime Component "Rubberband" Brunnian Links Identifying Knots within a List Cabling Burau's Theorem Further Knot Theory Software KnotPlot Knotscape Xknots Extending/Modifying KnotTheory` Bugs How to Edit this Manual...

Conway notation and KnotTheory`

KnotTheory` understands the Conway notation for knots and links (see [Conway] and down below), though the conversion between Conway notation and other knot presentations known to KnotTheory` (a necessary first step for using most of the KnotTheory` functionnality) requires the packages K2K (KNOT 2000, by M.Ochiai and N.Imafuji) and LinKnot (by S. Jablan and R. Sazdanovic). For the download and installation of the LinKnot package see Using the LinKnot package.

(For In[1] see Setup)

As in the section Using the LinKnot package, the first step is to add LinKnot to the Mathematica search path. This path will likely be different on your computer. (Note that you can also use Conway notations in KnotTheory` if you are using KnotTheory` and LinKnot "in parallel", as described in Using the LinKnot package.)

In[2]:=

AppendTo[$Path, "C:/bin/LinKnot/"];

In[3]:= ?ConwayNotation ConwayNotation[s] represents the knot or link whose Conway notation is the string s. ConwayNotation[K], where K is a knot or a link with up to 12 crossings, returns ConwayNotation[s], where s is a string containing the Conway notation of K.

In[4]:= ConwayNotation::about The program ConwayNotation relies on code from the LinKnot package by Slavik Jablan and Ramila Sazdanovic.

A well known example of a knot with an Alexander polynomial equal to the Alexander polynomial of the unknot is the (-3,5,7)-pretzel knot $K$. Let us verify that, check (using the Jones polynomial that $K$ is not the unknot and find a (rather unattractive) braid whose closure is $K$:

In[6]:=	DrawMorseLink[K = ConwayNotation["-3,5,7"]] // Show
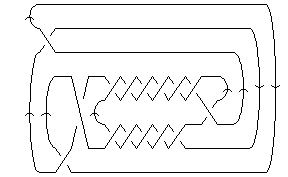
Out[6]=	-Graphics-

In[7]:=	Alexander[K][t]
Out[7]=	1

In[8]:=	Jones[K][q]
Out[8]=	-12 -11 -10 2 -8 -7 -5 -4 2 -2 1 q - q q - -- q - q q - q -- - q - 9 3 q q q

In[9]:=	br = BR[K]
Out[9]=	BR[14, {1, 2, 3, -4, -5, -6, -7, 8, -7, 6, 5, 4, -3, -2, -1, -6, -5, -4, -3, -2, 9, 8, 7, 6, -5, 4, -3, 7, -8, -7, -9, -8, 10, 9, -8, -11, -10, 12, 11, -10, 9, -8, -13, -12, -11, 10, 9, -8, -7, 6, -5, 4, -5, -7, 8, -7, -6, -7, -9, 8, -7, 6, 5, -4, 3, 2, -6, -7, -10, -9, 11, 10, -9, 8, -7, 6, 5, -4, 3, -6, 5, 4, -6, 5, 7, 6, -7, -8, 9, 8, -7, 12, -11, 10, -9, 13, -12, 11, -10}]

In[11]:=	BraidPlot[br] // Show
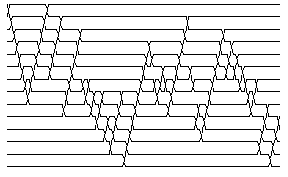
Out[11]=	-Graphics-

Some generalities about the Conway notation

Conway notation was introduced by J.H. Conway in 1967 (see [Conway]). The main building blocks for Conway notation are 4-tangles. A 4-tangle in a knot or link projection is a region in the projection plane ${\mathbb {R} }^{2}$ (or on the sphere $S^{3}$) surrounded with a circle such that the projection intersects with the circle exactly four times. The elementary tangles are:

Tangles can be combined and modified by a unary operation $a\mapsto -a$ and three binary operations: sum, product and ramification, taking tangles $a$, $b$ to new tangles $ab$, $a\,b$ and $a,b$. Here $-a$ is the image of $a$ under reflection in the NW-SE mirror line, $ab$ is obtained by placing $a$ and $b$ side by side with $a$ on the left and $b$ on the right. $a\,b$ is simply $(-a)b$, and finally, $a,b=(-a)(-b)$.

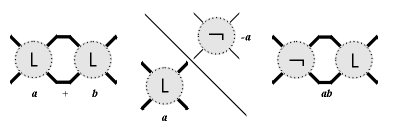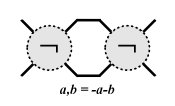Sum and product of tangles	Ramification of tangles

A rational tangle is any tangle obtained from the elementary tangles using only the operation of product. A rational knot or a rational link is the numerator closure of a rational tangle. A knot or link is called algebraic if it can be obtained as the closure of a tangle obtained from rational tangles using the operations above.

Knot or links that can not be obtained in this way are called non-algebraic. They can all be obtained in the following manner: start with a basic polyhedron $P$, a 4-valent graph without digons, with vertices numbered $1$ through $n$. Now substitute tangles $t_{1}$ through $t_{n}$ into these vertices.

The Conway notation for such knots and links consists of the symbol $ni^{\star }$ of a basic polyhedron $P$ where $n$ is the number of vertices and $i$ is the index of $P$ in some fixed list of basic polyhedra with $n$ vertices, followed by the symbols for the tangles $t_{1}$ through $t_{n}$ separated by dots.

For example, the knot 4_1 is denoted by "2 2", the knot 9_5 by "5 1 3", the link L5a1 is denoted by "2 1 2", the link L9a24 by "3 1,3,2" (all of them contain spaces between tangles), etc. A sequence of k pluses at the end of Conway symbol is denoted by k, and the sequence of k minuses by -k (e.g., knot 10_76 given in Conway notation as 3,3,2 is denoted by "3,3,2 2", and the mirror of the link L9n21 whose Conway notation is 3,2,2,2-- is given by "3,2,2,2 -2"). The space is used in the same way in all other symbols.

For the basic polyhedra with $N<10$ crossings the standard notation is used (.1 , 6*, 8*, 9*, where the symbol for 6* can be ommitted). For example, the knot 10_95 is denoted by ".2 1 0.2.2", and 10_101 by "2 1..2..2". For higher values of $N$ a notation is used in which the first number is the number of crossings, and the next is the ordering number of polyhedron (e.g., 101*, 102*, 103* for $N=10$ denoting 10*, 10**, 10***, respectively, and 111*, 112*, 113* for $N=11$ denoting 11*, 11**, 11***, respectively, etc.).

The order of basic polyhedra for $N=12$ corresponds to the list in [Caudron], so 121* to 1212* denote the basic polyhedra originally titled as 12A-12L. For $N>12$ the database of basic polyhedra is produced from the list of simple 4-regular 4-edge-connected but not 3-connected plane graphs generated by Brendan McKay using the program "plantri" written by Gunnar Brinkmann and Brendan McKay (http://cs.anu.edu.au/~bdm/plantri/). PolyBase.m is automatically downloaded and it contains basic polyhedra up to 16 crossings. In order to work with the basic polyhedra up to 20 vertices, one needs to open an additional database PolyBaseN.m, for $N=17$ to $N=20$ (by writing, e.g. <<PolyBase17.m or Needs["PolyBase17.m"] for $N=17$).

Note: Together with the classical notation, Conway symbols are given in the book Knots and Links by D.~Rolfsen. However if you try to draw some knots or links from their Conway symbols the obtained projection might be non-isomorphic with the one given in Rolfsen, for example knot 9_15 denoted in Conway notation as 2 3 2 2 gives projection with 5, and not 4 digons.

[Caudron] ^  A. Caudron, Classification des noeuds et des enlancements. Public. Math. d'Orsay 82. Orsay: Univ. Paris Sud, Dept. Math., 1982.

[Conway] ^  J. H. Conway, An Enumeration of Knots and Links, and Some of Their Algebraic Properties. In Computation Problems in Abstract Algebra (Ed. J. Leech). Oxford, England: Pergamon Press, pp. 329-358, 1967.