Three Dimensional Invariants: Difference between revisions
No edit summary |
No edit summary |
||
| Line 52: | Line 52: | ||
<!--END--> |
<!--END--> |
||
{{Knot Image Quadruple|9_10|gif|9_13|gif|9_35|gif|9_38|gif}} |
|||
<gallery> |
|||
|9_10.gif|[[9_10]] |
|||
|9_13.gif|[[9_13]] |
|||
|9_35.gif|[[9_35]] |
|||
|9_38.gif|[[9_38]] |
|||
</gallery> |
|||
<!--$$?ThreeGenus$$--> |
<!--$$?ThreeGenus$$--> |
||
| Line 150: | Line 145: | ||
<!--END--> |
<!--END--> |
||
<gallery> |
|||
{{Knot Image Quadruple|9_24|gif|9_28|gif|9_30|gif|9_34|gif}} |
|||
|9_24.gif|[[9_24]] |
|||
|9_28.gif|[[9_28]] |
|||
|9_30.gif|[[9_30]] |
|||
|9_34.gif|[[9_34]] |
|||
</gallery> |
|||
<!--$$Alexander[#][t]& /@ Ks$$--> |
<!--$$Alexander[#][t]& /@ Ks$$--> |
||
Revision as of 03:39, 3 September 2005
(For In[1] see Setup)
|
| ||||||||
The unknotting number of a knot is the minimal number of crossing changes needed in order to unknot .
|
| ||||||||
Of the 512 knots whose unknotting number is known to KnotTheory`, 197 have unknotting number 1, 247 have unknotting number 2, 54 have unknotting number 3, 12 have unknotting number 4 and 1 has unknotting number 5:
In[5]:=
|
Plus @@ u /@ Cases[UnknottingNumber /@ AllKnots[], _Integer]
|
Out[5]=
|
u[0] + 197 u[1] + 247 u[2] + 54 u[3] + 12 u[4] + u[5]
|
There are 4 knots with up to 9 crossings whose unknotting number is unknown:
In[6]:=
|
Select[AllKnots[],
Crossings[#] <= 9 && Head[UnknottingNumber[#]] === List &
]
|
Out[6]=
|
{Knot[9, 10], Knot[9, 13], Knot[9, 35], Knot[9, 38]}
|
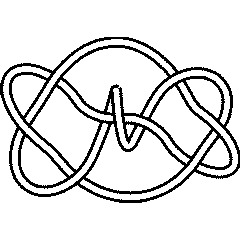 9_10 |
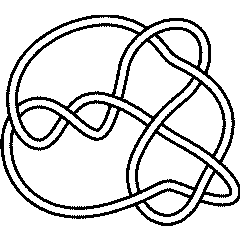 9_13 |
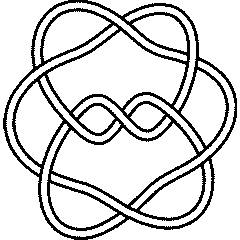 9_35 |
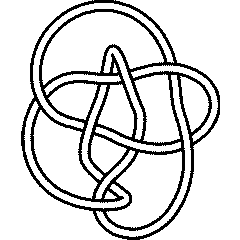 9_38 |
|
| ||||||||
The bridge index' of a knot is the minimal number of local maxima (or local minima) in a generic smooth embedding of in .
|
| ||||||||
An often studied class of knots is the class of 2-bridge knots, knots whose bridge index is 2. Of the 49 9-crossings knots, 24 are 2-bridge:
In[11]:=
|
Select[AllKnots[], Crossings[#] == 9 && BridgeIndex[#] == 2 &]
|
Out[11]=
|
{Knot[9, 1], Knot[9, 2], Knot[9, 3], Knot[9, 4], Knot[9, 5],
Knot[9, 6], Knot[9, 7], Knot[9, 8], Knot[9, 9], Knot[9, 10],
Knot[9, 11], Knot[9, 12], Knot[9, 13], Knot[9, 14], Knot[9, 15],
Knot[9, 17], Knot[9, 18], Knot[9, 19], Knot[9, 20], Knot[9, 21],
Knot[9, 23], Knot[9, 26], Knot[9, 27], Knot[9, 31]}
|
The super bridge index of a knot is the minimal number, in a generic smooth embedding of in , of the maximal number of local maxima (or local minima) in a rigid rotation of that projection.
|
| ||||||||
|
| ||||||||
In[16]:=
|
Profile[K_] := Profile[
SymmetryType[K], UnknottingNumber[K], ThreeGenus[K],
BridgeIndex[K], SuperBridgeIndex[K], NakanishiIndex[K]
]
|
In[17]:=
|
Profile[Knot[9,24]]
|
Out[17]=
|
Profile[Reversible, 1, 3, 3, {4, 6}, 1]
|
In[18]:=
|
Ks = Select[AllKnots[], (Crossings[#] == 9 && Profile[#]==Profile[Knot[9,24]])&]
|
Out[18]=
|
{Knot[9, 24], Knot[9, 28], Knot[9, 30], Knot[9, 34]}
|
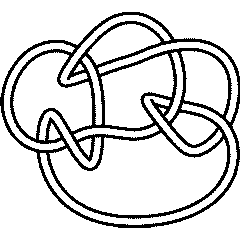 9_24 |
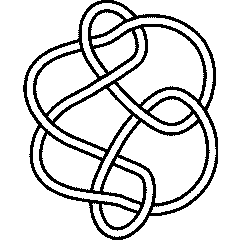 9_28 |
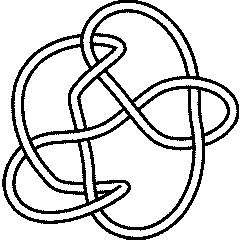 9_30 |
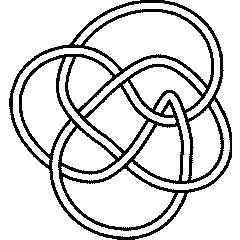 9_34 |
In[19]:=
|
Alexander[#][t]& /@ Ks
|
Out[19]=
|
-3 5 10 2 3
{13 - t + -- - -- - 10 t + 5 t - t ,
2 t
t
-3 5 12 2 3
-15 + t - -- + -- + 12 t - 5 t + t ,
2 t
t
-3 5 12 2 3
17 - t + -- - -- - 12 t + 5 t - t ,
2 t
t
-3 6 16 2 3
23 - t + -- - -- - 16 t + 6 t - t }
2 t
t
|

