The Multivariable Alexander Polynomial

KnotTheory`/Navigation  The Mathematica Package KnotTheory` Acknowledgement Setup Naming and Enumeration Presentations Planar Diagrams Some further details Gauss Codes DT (Dowker-Thistlethwaite) Codes Braid Representatives MorseLink Presentations Arc Presentations Conway Notation Graphical Input Graphical Output Drawing Planar Diagrams How does it work? Drawing MorseLink Presentations Drawing Braids Structure and Operations Invariants Invariants from Braid Theory Three Dimensional Invariants The Alexander-Conway Polynomial The Multivariable Alexander Polynomial The Determinant and the Signature The Jones Polynomial How is the Jones polynomial computed? The Coloured Jones Polynomials The A2 Invariant Quantum knot invariants The HOMFLY-PT Polynomial The Kauffman Polynomial Finite Type (Vassiliev) Invariants Khovanov Homology Heegaard Floer Knot Homology R-Matrix Invariants Extras Included with KnotTheory` Drawing with TubePlot Standalone_TubePlot Using the LinKnot package WikiLink QuantumGroups` Lightly Documented Features A Sample KnotTheory` Session Further Usage Example Prime Links with a Non-Prime Component "Rubberband" Brunnian Links Identifying Knots within a List Cabling Burau's Theorem Further Knot Theory Software KnotPlot Knotscape Xknots Extending/Modifying KnotTheory` Bugs How to Edit this Manual...

(For In[1] see Setup)

In[1]:= ?MultivariableAlexander MultivariableAlexander[L][t] returns the multivariable Alexander polynomial of a link L as a function of the variable t[1], t[2], ..., t[c], where c is the number of components of L. MultivariableAlexander[L, Program -> prog][t] uses the program prog to perform the computation. The currently available programs are "MVA1", written by Dan Carney in Toronto in the summer of 2005, and the faster "MVA2" (default), written by Jana Archibald in Toronto in 2008-9.

In[2]:= MultivariableAlexander::about The multivariable Alexander program "MVA1" was written by Dan Carney at the University of Toronto in the summer of 2005; "MVA2" was written by Jana Archibald in Toronto in 2008-9.

L8a21

The link L8a21 is symmetric under cyclic permutations of its components but not under interchanging two adjacent components. It is amusing to see how this is reflected in its multivariable Alexander polynomial:

In[3]:=	mva = MultivariableAlexander[Link[8, Alternating, 21]][t] /. { t[1] -> t1, t[2] -> t2, t[3] -> t4, t[4] -> t3 }
Out[3]=	(-t1 - t2 + t1 t2 - t3 + 2 t1 t3 + t2 t3 - t1 t2 t3 - t4 + t1 t4 + 2 t2 t4 - t1 t2 t4 + t3 t4 - t1 t3 t4 - t2 t3 t4) / (Sqrt[t1] Sqrt[t2] Sqrt[t3] Sqrt[t4])

In[4]:=	mva - (mva /. {t1->t2, t2->t3, t3->t4, t4->t1})
Out[4]=	0

In[5]:=	Simplify[mva - (mva /. {t1->t2, t2->t1})]
Out[5]=	(t1 - t2) (t3 - t4) ----------------------------------- Sqrt[t1] Sqrt[t2] Sqrt[t3] Sqrt[t4]

But notice the funny labelling of the components! At the moment there is no way to tell MultivariableAlexander which variable is to be associated with what variable so MultivariableAlexander chooses an arbitrary ordering of tha variables. Hence we had to rename t[3] to be t4 and t[4] to be t3.

(To be precise, MultivariableAlexander orders the components so that its output would be lexicographically minimal among all possible orderings. This way it is at least guaranteed that different presentations for the same link will yield the same output for MultivariableAlexander.)

Links with Vanishing Multivariable Alexander Polynomial

There are 11 links with up to 11 crossings whose multivariable Alexander polynomial is $0$. Here they are:

In[6]:=	Select[AllLinks[], (MultivariableAlexander[#][t] == 0) &]
Out[6]=	{Link[9, NonAlternating, 27], Link[10, NonAlternating, 32], Link[10, NonAlternating, 36], Link[10, NonAlternating, 107], Link[11, NonAlternating, 244], Link[11, NonAlternating, 247], Link[11, NonAlternating, 334], Link[11, NonAlternating, 381], Link[11, NonAlternating, 396], Link[11, NonAlternating, 404], Link[11, NonAlternating, 406]}

L9n27

L10n32

L10n36

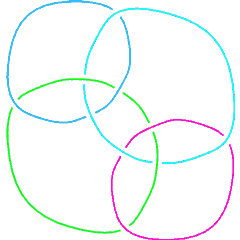L10n107

L11n244

L11n247

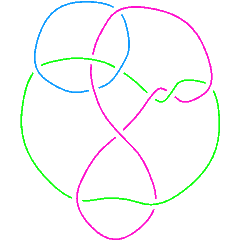L11n334

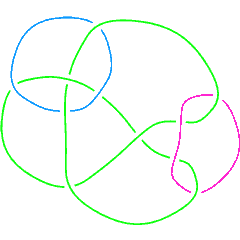L11n381

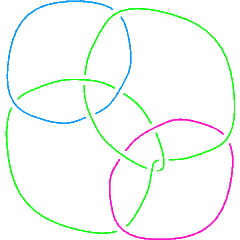L11n396

L11n404

L11n406

Dror doesn't understand the multivariable Alexander polynomial well enough to give simple topological reasons for the vanishing of the said polynomial for these knots. (Though see the Talk Page).

Detecting a Link Using the Multivariable Alexander Polynomial

A mystery link

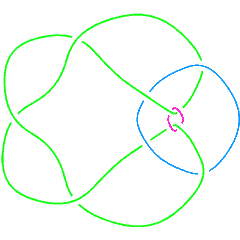
On May 1, 2007 AnonMoos asked Dror if he could identify the link in the figure on the right. So Dror typed:

In[7]:=	mva = MultivariableAlexander[L = PD[ X[1, 16, 2, 17], X[3, 15, 4, 14], X[5, 8, 6, 9], X[7, 21, 8, 20], X[9, 22, 10, 13], X[11, 2, 12, 3], X[13, 18, 14, 19], X[15, 12, 16, 1], X[17, 11, 18, 10], X[19, 4, 20, 5], X[21, 7, 22, 6] ]][t]
Out[7]=	2 -(((-1 + t[1]) (-1 + t[2]) (1 - 2 t[1] + t[1] - 2 t[2] + 2 t[1] t[2] - 2 2 2 2 2 2 t[1] t[2] + t[2] - 2 t[1] t[2] + t[1] t[2] )) / 3/2 3/2 (t[1] t[2] ))

We don't know whether our mystery link appears in the link table as is, or as a mirror, or with its two components switched. Hence we let AllPossibilities contain the multivariable Alexander polynomials of all those possibilities:

In[8]:=	AllPossibilities = Union[Flatten[ {mva, -mva} /. {{}, {t[1] -> t[2], t[2] -> t[1]}} ]]
Out[8]=	2 {-(((-1 + t[1]) (-1 + t[2]) (1 - 2 t[1] + t[1] - 2 t[2] + 2 2 2 2 2 2 t[1] t[2] - 2 t[1] t[2] + t[2] - 2 t[1] t[2] + t[1] t[2] 3/2 3/2 )) / (t[1] t[2] )), 2 ((-1 + t[1]) (-1 + t[2]) (1 - 2 t[1] + t[1] - 2 t[2] + 2 t[1] t[2] - 2 2 2 2 2 2 t[1] t[2] + t[2] - 2 t[1] t[2] + t[1] t[2] )) / 3/2 3/2 (t[1] t[2] )}

Finally, let us locate our link in the link table:

In[9]:=	Select[ AllLinks[], MemberQ[AllPossibilities, MultivariableAlexander[#][t]] & ]
Out[9]=	{Link[11, Alternating, 289]}

And just to be sure,

In[10]:=	{Jones[L][q], Jones[Link[11, Alternating, 289]][q]}
Out[10]=	-(17/2) 4 8 12 16 18 17 15 {q - ----- + ----- - ----- + ---- - ---- + ---- - ---- + 15/2 13/2 11/2 9/2 7/2 5/2 3/2 q q q q q q q 10 3/2 5/2 ------- - 7 Sqrt[q] + 3 q - q , Sqrt[q] -(5/2) 3 7 3/2 5/2 -q + ---- - ------- + 10 Sqrt[q] - 15 q + 17 q - 3/2 Sqrt[q] q 7/2 9/2 11/2 13/2 15/2 17/2 18 q + 16 q - 12 q + 8 q - 4 q + q }

Thus the mystery link is the mirror image of L11a289.