Three Dimensional Invariants: Difference between revisions
| Line 127: | Line 127: | ||
A Seifert surface for a knot <math>K \subset S^3</math> is a compact oriented surface <math>L \subset S^3</math> |
A Seifert surface for a knot <math>K \subset S^3</math> is a compact oriented surface <math>L \subset S^3</math> |
||
with boundary <math>\partial L=K</math>. Seifert surfaces exist, but are not unique. The SeifertView programme |
with boundary <math>\partial L=K</math>. Seifert surfaces exist, but are not unique. The [http://www.win.tue.nl/~vanwijk/seifertview/ SeifertView programme] is a visual implementation of the algorithm of Seifert (1934) for |
||
http://www.win.tue.nl/~vanwijk/seifertview/ is a visual implementation of the algorithm of Seifert (1934) for |
|||
the construction of a Seifert surface from a knot projection. The 3-genus of a knot is the minimal genus of a |
the construction of a Seifert surface from a knot projection. The 3-genus of a knot is the minimal genus of a |
||
Seifert surface for that knot. |
Seifert surface for that knot. |
||
Revision as of 07:00, 16 April 2006
(For In[1] see Setup)
Symmetry Type
|
| ||||||||
The inverse of a knot is the knot obtained from it by reversing its parametrization. The mirror of A knot is obtained from by reversing the orientation of the ambient space, or, alternatively, by flipping all the crossings of .
A knot is called "fully amphicheiral" if it is equal to its inverse and also to its mirror. The first knot with this property is
In[4]:=
|
Select[AllKnots[],
(SymmetryType[#] == FullyAmphicheiral) &, 1]
|
Out[4]=
|
{Knot[4, 1]}
|
A knot is called "reversible" if it is equal to its inverse yet it different from its mirror (and hence also from the inverse of its mirror). Many knots have this property; indeed, the first one is:
In[5]:=
|
Select[AllKnots[],
(SymmetryType[#] == Reversible) &, 1]
|
Out[5]=
|
{Knot[3, 1]}
|
A knot is called "positive amphicheiral" if it is different from its inverse but equal to its mirror. There are no such knots with up to 11 crossings.
A knot is called "negative amphicheiral" if it is different from its inverse and its mirror, yet it is equal to the inverse of its mirror. The first knot with this property is
In[6]:=
|
Select[AllKnots[],
(SymmetryType[#] == NegativeAmphicheiral) &, 1]
|
Out[6]=
|
{Knot[8, 17]}
|
Finally, if a knot is different from its inverse, its mirror and from the inverse of its mirror, it is "chiral". The first such knot is
In[7]:=
|
Select[AllKnots[],
(SymmetryType[#] == Chiral) &, 1]
|
Out[7]=
|
{Knot[9, 32]}
|
It is a amusing to take "symmetry type" statistics on all the prime knots with up to 11 crossings:
In[8]:=
|
Plus @@ (SymmetryType /@ Rest[AllKnots[]])
|
Out[8]=
|
216 Chiral + 13 FullyAmphicheiral + 7 NegativeAmphicheiral +
565 Reversible
|
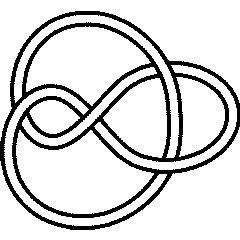 4_1 |
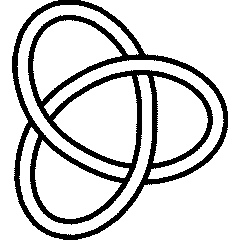 3_1 |
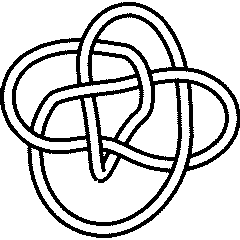 8_17 |
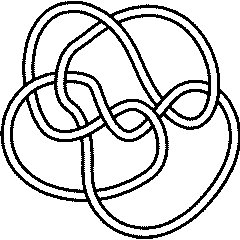 9_32 |
Unknotting Number
The unknotting number of a knot is the minimal number of crossing changes needed in order to unknot .
|
| ||||||||
Of the 512 knots whose unknotting number is known to KnotTheory`, 197 have unknotting number 1, 247 have unknotting number 2, 54 have unknotting number 3, 12 have unknotting number 4 and 1 has unknotting number 5:
In[11]:=
|
Plus @@ u /@ Cases[UnknottingNumber /@ AllKnots[], _Integer]
|
Out[11]=
|
u[0] + 197 u[1] + 247 u[2] + 54 u[3] + 12 u[4] + u[5]
|
There are 4 knots with up to 9 crossings whose unknotting number is unknown:
In[12]:=
|
Select[AllKnots[],
Crossings[#] <= 9 && Head[UnknottingNumber[#]] === List &
]
|
Out[12]=
|
{Knot[9, 10], Knot[9, 13], Knot[9, 35], Knot[9, 38]}
|
 9_10 |
 9_13 |
 9_35 |
 9_38 |
3-Genus
A Seifert surface for a knot is a compact oriented surface with boundary . Seifert surfaces exist, but are not unique. The SeifertView programme is a visual implementation of the algorithm of Seifert (1934) for the construction of a Seifert surface from a knot projection. The 3-genus of a knot is the minimal genus of a Seifert surface for that knot.
|
| ||||||||
The highest 3-genus of the knots known to KnotTheory` is , and there is only one knot with up to 11 crossings whose 3-genus is 5:
In[15]:=
|
Max[ThreeGenus /@ AllKnots[]]
|
Out[15]=
|
5
|
In[16]:=
|
Select[AllKnots[], ThreeGenus[#] == 5 &]
|
Out[16]=
|
{Knot[11, Alternating, 367]}
|
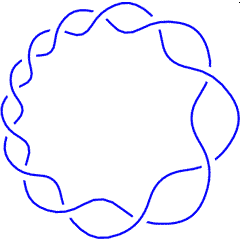 K11a367 |
 T(11,2) |
(K11a367 is, of couse, also known as the torus knot T(11,2)).
The Conway knot K11n34 is the closure of the braid BR[4, {1, 1, 2, -3, 2, 1, -3, -2, -2, -3, -3}]. Let us compute its 3-genus and compare it with the 3-genus of its mutant companion, the Kinoshita-Terasaka knot K11n42:
In[17]:=
|
ThreeGenus[BR[4, {1, 1, 2, -3, 2, 1, -3, -2, -2, -3, -3}]]
|
Out[17]=
|
3
|
In[18]:=
|
ThreeGenus[Knot[11, NonAlternating, 42]]
|
Out[18]=
|
2
|
 K11n34 |
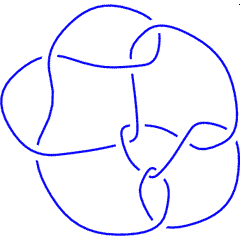 K11n32 |
Bridge Index
The bridge index' of a knot is the minimal number of local maxima (or local minima) in a generic smooth embedding of in .
|
| ||||||||
An often studied class of knots is the class of 2-bridge knots, knots whose bridge index is 2. Of the 49 prime 9-crossings knots, 24 are 2-bridge:
In[21]:=
|
Select[AllKnots[], Crossings[#] == 9 && BridgeIndex[#] == 2 &]
|
Out[21]=
|
{Knot[9, 1], Knot[9, 2], Knot[9, 3], Knot[9, 4], Knot[9, 5],
Knot[9, 6], Knot[9, 7], Knot[9, 8], Knot[9, 9], Knot[9, 10],
Knot[9, 11], Knot[9, 12], Knot[9, 13], Knot[9, 14], Knot[9, 15],
Knot[9, 17], Knot[9, 18], Knot[9, 19], Knot[9, 20], Knot[9, 21],
Knot[9, 23], Knot[9, 26], Knot[9, 27], Knot[9, 31]}
|
Super Bridge Index
The super bridge index of a knot is the minimal number, in a generic smooth embedding of in , of the maximal number of local maxima (or local minima) in a rigid rotation of that projection.
|
| ||||||||
Nakanishi Index
|
| ||||||||
Synthesis
In[26]:=
|
Profile[K_] := Profile[
SymmetryType[K], UnknottingNumber[K], ThreeGenus[K],
BridgeIndex[K], SuperBridgeIndex[K], NakanishiIndex[K]
]
|
In[27]:=
|
Profile[Knot[9,24]]
|
Out[27]=
|
Profile[Reversible, 1, 3, 3, {4, 6}, 1]
|
In[28]:=
|
Ks = Select[AllKnots[], (Crossings[#] == 9 && Profile[#]==Profile[Knot[9,24]])&]
|
Out[28]=
|
{Knot[9, 24], Knot[9, 28], Knot[9, 30], Knot[9, 34]}
|
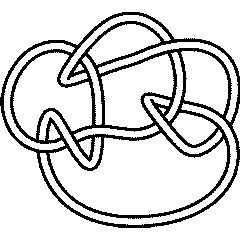 9_24 |
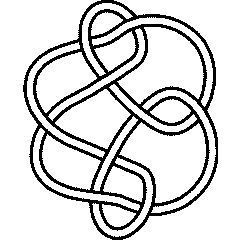 9_28 |
 9_30 |
 9_34 |
In[29]:=
|
Alexander[#][t]& /@ Ks
|
Out[29]=
|
-3 5 10 2 3
{13 - t + -- - -- - 10 t + 5 t - t ,
2 t
t
-3 5 12 2 3
-15 + t - -- + -- + 12 t - 5 t + t ,
2 t
t
-3 5 12 2 3
17 - t + -- - -- - 12 t + 5 t - t ,
2 t
t
-3 6 16 2 3
23 - t + -- - -- - 16 t + 6 t - t }
2 t
t
|





