Three Dimensional Invariants: Difference between revisions
DrorsRobot (talk | contribs) No edit summary |
No edit summary |
||
| Line 17: | Line 17: | ||
A knot is called "fully amphicheiral" if it is equal to its inverse and also to its mirror. The first knot with this property is |
A knot is called "fully amphicheiral" if it is equal to its inverse and also to its mirror. The first knot with this property is |
||
<!--$$Select[AllKnots[], |
<!--$$Select[AllKnots[], |
||
(SymmetryType[#] == FullyAmphicheiral) &, 1]$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{InOut| |
{{InOut| |
||
n = 4 | |
n = 4 | |
||
in = <nowiki>Select[AllKnots[], |
in = <nowiki>Select[AllKnots[], |
||
(SymmetryType[#] == FullyAmphicheiral) &, 1]</nowiki> | |
|||
out= <nowiki>{Knot[4, 1]}</nowiki>}} |
out= <nowiki>{Knot[4, 1]}</nowiki>}} |
||
<!--END--> |
<!--END--> |
||
| Line 27: | Line 29: | ||
A knot is called "reversible" if it is equal to its inverse yet it different from its mirror (and hence also from the inverse of its mirror). Many knots have this property; indeed, the first one is: |
A knot is called "reversible" if it is equal to its inverse yet it different from its mirror (and hence also from the inverse of its mirror). Many knots have this property; indeed, the first one is: |
||
<!--$$Select[AllKnots[], |
<!--$$Select[AllKnots[], |
||
(SymmetryType[#] == Reversible) &, 1]$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{InOut| |
{{InOut| |
||
n = 5 | |
n = 5 | |
||
in = <nowiki>Select[AllKnots[], |
in = <nowiki>Select[AllKnots[], |
||
(SymmetryType[#] == Reversible) &, 1]</nowiki> | |
|||
out= <nowiki>{Knot[3, 1]}</nowiki>}} |
out= <nowiki>{Knot[3, 1]}</nowiki>}} |
||
<!--END--> |
<!--END--> |
||
| Line 39: | Line 43: | ||
A knot is called "negative amphicheiral" if it is different from its inverse and its mirror, yet it is equal to the inverse of its mirror. The first knot with this property is |
A knot is called "negative amphicheiral" if it is different from its inverse and its mirror, yet it is equal to the inverse of its mirror. The first knot with this property is |
||
<!--$$Select[AllKnots[], |
<!--$$Select[AllKnots[], |
||
(SymmetryType[#] == NegativeAmphicheiral) &, 1]$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{InOut| |
{{InOut| |
||
| Line 49: | Line 54: | ||
Finally, if a knot is different from its inverse, its mirror and from the inverse of its mirror, it is "chiral". The first such knot is |
Finally, if a knot is different from its inverse, its mirror and from the inverse of its mirror, it is "chiral". The first such knot is |
||
<!--$$Select[AllKnots[], |
<!--$$Select[AllKnots[], |
||
(SymmetryType[#] == Chiral) &, 1]$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{InOut| |
{{InOut| |
||
| Line 68: | Line 74: | ||
565 Reversible</nowiki>}} |
565 Reversible</nowiki>}} |
||
<!--END--> |
<!--END--> |
||
{{Knot Image Quadruple|4_1|gif|3_1|gif|8_17|gif|9_32|gif}} |
|||
The ''unknotting number'' of a knot <math>K</math> is the minimal number of crossing changes needed in order to unknot <math>K</math>. |
The ''unknotting number'' of a knot <math>K</math> is the minimal number of crossing changes needed in order to unknot <math>K</math>. |
||
Revision as of 22:15, 18 September 2005
(For In[1] see Setup)
|
| ||||||||
The inverse of a knot is the knot obtained from it by reversing its parametrization. The mirror of A knot is obtained from by reversing the orientation of the ambient space, or, alternatively, by flipping all the crossings of .
A knot is called "fully amphicheiral" if it is equal to its inverse and also to its mirror. The first knot with this property is
In[4]:=
|
Select[AllKnots[],
(SymmetryType[#] == FullyAmphicheiral) &, 1]
|
Out[4]=
|
{Knot[4, 1]}
|
A knot is called "reversible" if it is equal to its inverse yet it different from its mirror (and hence also from the inverse of its mirror). Many knots have this property; indeed, the first one is:
In[5]:=
|
Select[AllKnots[],
(SymmetryType[#] == Reversible) &, 1]
|
Out[5]=
|
{Knot[3, 1]}
|
A knot is called "positive amphicheiral" if it is different from its inverse but equal to its mirror. There are no such knots with up to 11 crossings.
A knot is called "negative amphicheiral" if it is different from its inverse and its mirror, yet it is equal to the inverse of its mirror. The first knot with this property is
In[6]:=
|
Select[AllKnots[], (SymmetryType[#] == NegativeAmphicheiral) &, 1]
|
Out[6]=
|
{Knot[8, 17]}
|
Finally, if a knot is different from its inverse, its mirror and from the inverse of its mirror, it is "chiral". The first such knot is
In[7]:=
|
Select[AllKnots[], (SymmetryType[#] == Chiral) &, 1]
|
Out[7]=
|
{Knot[9, 32]}
|
It is a amusing to take "symmetry type" statistics on all the prime knots with up to 11 crossings:
In[8]:=
|
Plus @@ (SymmetryType /@ Rest[AllKnots[]])
|
Out[8]=
|
216 Chiral + 13 FullyAmphicheiral + 7 NegativeAmphicheiral +
565 Reversible
|
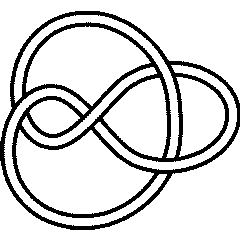 4_1 |
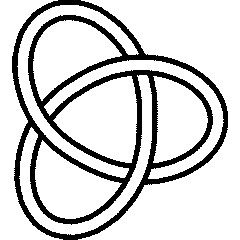 3_1 |
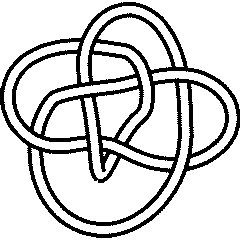 8_17 |
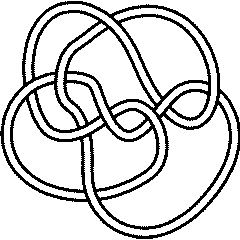 9_32 |
The unknotting number of a knot is the minimal number of crossing changes needed in order to unknot .
|
| ||||||||
Of the 512 knots whose unknotting number is known to KnotTheory`, 197 have unknotting number 1, 247 have unknotting number 2, 54 have unknotting number 3, 12 have unknotting number 4 and 1 has unknotting number 5:
In[11]:=
|
Plus @@ u /@ Cases[UnknottingNumber /@ AllKnots[], _Integer]
|
Out[11]=
|
u[0] + 197 u[1] + 247 u[2] + 54 u[3] + 12 u[4] + u[5]
|
There are 4 knots with up to 9 crossings whose unknotting number is unknown:
In[12]:=
|
Select[AllKnots[],
Crossings[#] <= 9 && Head[UnknottingNumber[#]] === List &
]
|
Out[12]=
|
{Knot[9, 10], Knot[9, 13], Knot[9, 35], Knot[9, 38]}
|
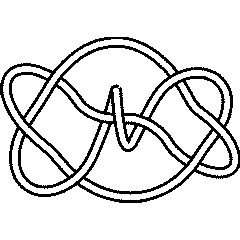 9_10 |
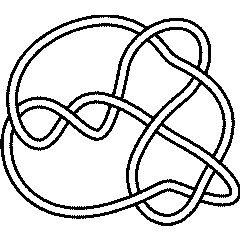 9_13 |
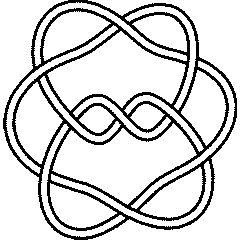 9_35 |
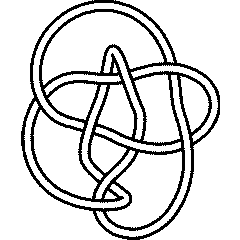 9_38 |
|
| ||||||||
The bridge index' of a knot is the minimal number of local maxima (or local minima) in a generic smooth embedding of in .
|
| ||||||||
An often studied class of knots is the class of 2-bridge knots, knots whose bridge index is 2. Of the 49 9-crossings knots, 24 are 2-bridge:
In[17]:=
|
Select[AllKnots[], Crossings[#] == 9 && BridgeIndex[#] == 2 &]
|
Out[17]=
|
{Knot[9, 1], Knot[9, 2], Knot[9, 3], Knot[9, 4], Knot[9, 5],
Knot[9, 6], Knot[9, 7], Knot[9, 8], Knot[9, 9], Knot[9, 10],
Knot[9, 11], Knot[9, 12], Knot[9, 13], Knot[9, 14], Knot[9, 15],
Knot[9, 17], Knot[9, 18], Knot[9, 19], Knot[9, 20], Knot[9, 21],
Knot[9, 23], Knot[9, 26], Knot[9, 27], Knot[9, 31]}
|
The super bridge index of a knot is the minimal number, in a generic smooth embedding of in , of the maximal number of local maxima (or local minima) in a rigid rotation of that projection.
|
| ||||||||
|
| ||||||||
In[22]:=
|
Profile[K_] := Profile[
SymmetryType[K], UnknottingNumber[K], ThreeGenus[K],
BridgeIndex[K], SuperBridgeIndex[K], NakanishiIndex[K]
]
|
In[23]:=
|
Profile[Knot[9,24]]
|
Out[23]=
|
Profile[Reversible, 1, 3, 3, {4, 6}, 1]
|
In[24]:=
|
Ks = Select[AllKnots[], (Crossings[#] == 9 && Profile[#]==Profile[Knot[9,24]])&]
|
Out[24]=
|
{Knot[9, 24], Knot[9, 28], Knot[9, 30], Knot[9, 34]}
|
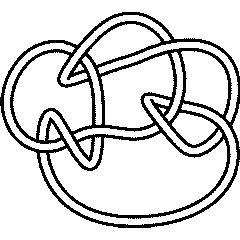 9_24 |
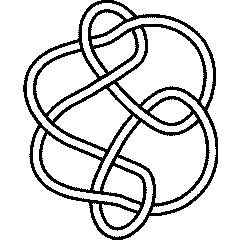 9_28 |
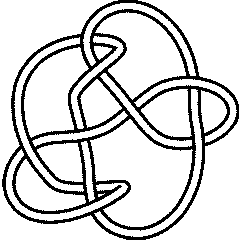 9_30 |
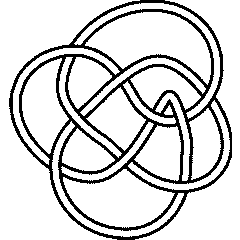 9_34 |
In[25]:=
|
Alexander[#][t]& /@ Ks
|
Out[25]=
|
-3 5 10 2 3
{13 - t + -- - -- - 10 t + 5 t - t ,
2 t
t
-3 5 12 2 3
-15 + t - -- + -- + 12 t - 5 t + t ,
2 t
t
-3 5 12 2 3
17 - t + -- - -- - 12 t + 5 t - t ,
2 t
t
-3 6 16 2 3
23 - t + -- - -- - 16 t + 6 t - t }
2 t
t
|

