Three Dimensional Invariants

KnotTheory`/Navigation  The Mathematica Package KnotTheory` Acknowledgement Setup Naming and Enumeration Presentations Planar Diagrams Some further details Gauss Codes DT (Dowker-Thistlethwaite) Codes Braid Representatives MorseLink Presentations Arc Presentations Conway Notation Graphical Input Graphical Output Drawing Planar Diagrams How does it work? Drawing MorseLink Presentations Drawing Braids Structure and Operations Invariants Invariants from Braid Theory Three Dimensional Invariants The Alexander-Conway Polynomial The Multivariable Alexander Polynomial The Determinant and the Signature The Jones Polynomial How is the Jones polynomial computed? The Coloured Jones Polynomials The A2 Invariant Quantum knot invariants The HOMFLY-PT Polynomial The Kauffman Polynomial Finite Type (Vassiliev) Invariants Khovanov Homology Heegaard Floer Knot Homology R-Matrix Invariants Extras Included with KnotTheory` Drawing with TubePlot Standalone_TubePlot Using the LinKnot package WikiLink QuantumGroups` Lightly Documented Features A Sample KnotTheory` Session Further Usage Example Prime Links with a Non-Prime Component "Rubberband" Brunnian Links Identifying Knots within a List Cabling Burau's Theorem Further Knot Theory Software KnotPlot Knotscape Xknots Extending/Modifying KnotTheory` Bugs How to Edit this Manual...

(For In[1] see Setup)

Symmetry Type

In[2]:= ?SymmetryType SymmetryType[K] returns the symmetry type of the knot K, if known to KnotTheory`. The possible types are: Reversible, FullyAmphicheiral, NegativeAmphicheiral and Chiral.

In[3]:= SymmetryType::about The symmetry type data known to KnotTheory` is taken from Charles Livingston's "Table of Knot Invariants", http://www.indiana.edu/~knotinfo/.

The inverse of a knot $K$ is the knot obtained from it by reversing its parametrization. The mirror of A knot $K$ is obtained from $K$ by reversing the orientation of the ambient space, or, alternatively, by flipping all the crossings of $K$.

A knot is called "fully amphicheiral" if it is equal to its inverse and also to its mirror. The first knot with this property is

In[4]:=	Select[AllKnots[], (SymmetryType[#] == FullyAmphicheiral) &, 1]
Out[4]=	{Knot[4, 1]}

A knot is called "reversible" if it is equal to its inverse yet it different from its mirror (and hence also from the inverse of its mirror). Many knots have this property; indeed, the first one is:

In[5]:=	Select[AllKnots[], (SymmetryType[#] == Reversible) &, 1]
Out[5]=	{Knot[3, 1]}

A knot is called "positive amphicheiral" if it is different from its inverse but equal to its mirror. There are no such knots with up to 11 crossings.

A knot is called "negative amphicheiral" if it is different from its inverse and its mirror, yet it is equal to the inverse of its mirror. The first knot with this property is

In[6]:=	Select[AllKnots[], (SymmetryType[#] == NegativeAmphicheiral) &, 1]
Out[6]=	{Knot[8, 17]}

Finally, if a knot is different from its inverse, its mirror and from the inverse of its mirror, it is "chiral". The first such knot is

In[7]:=	Select[AllKnots[], (SymmetryType[#] == Chiral) &, 1]
Out[7]=	{Knot[9, 32]}

It is a amusing to take "symmetry type" statistics on all the prime knots with up to 11 crossings:

In[8]:=	Plus @@ (SymmetryType /@ Rest[AllKnots[]])
Out[8]=	216 Chiral + 13 FullyAmphicheiral + 7 NegativeAmphicheiral + 565 Reversible

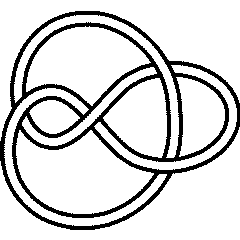4_1

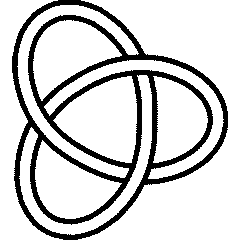3_1

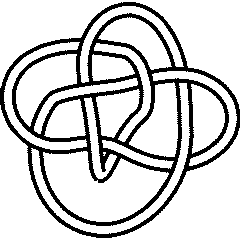8_17

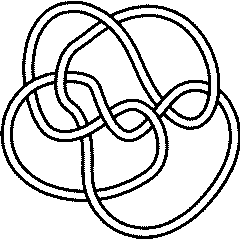9_32

Unknotting Number

The unknotting number of a knot $K$ is the minimal number of crossing changes needed in order to unknot $K$.

In[9]:= ?UnknottingNumber UnknottingNumber[K] returns the unknotting number of the knot K, if known to KnotTheory`. If only a range of possible values is known, a list of the form {min, max} is returned.

In[10]:= UnknottingNumber::about The unknotting numbers of torus knots are due to ???. All other unknotting numbers known to KnotTheory` are taken from Charles Livingston's "Table of Knot Invariants", http://www.indiana.edu/~knotinfo/.

Of the 512 knots whose unknotting number is known to KnotTheory`, 197 have unknotting number 1, 247 have unknotting number 2, 54 have unknotting number 3, 12 have unknotting number 4 and 1 has unknotting number 5:

In[11]:=	Plus @@ u /@ Cases[UnknottingNumber /@ AllKnots[], _Integer]
Out[11]=	u[0] + 197 u[1] + 247 u[2] + 54 u[3] + 12 u[4] + u[5]

There are 4 knots with up to 9 crossings whose unknotting number is unknown:

In[12]:=	Select[AllKnots[], Crossings[#] <= 9 && Head[UnknottingNumber[#]] === List & ]
Out[12]=	{Knot[9, 10], Knot[9, 13], Knot[9, 35], Knot[9, 38]}

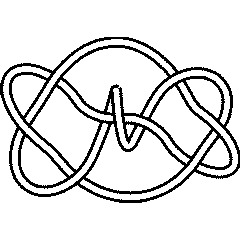9_10

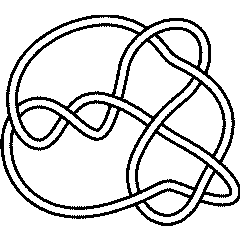9_13

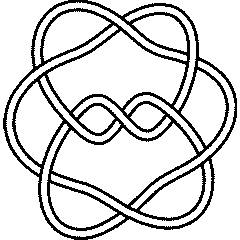9_35

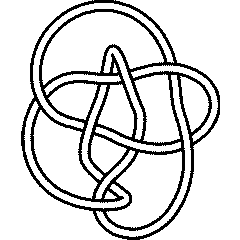9_38

3-Genus

The 3-genus of a knot is the minimal genus of a Seifert surface for that knot.

In[13]:= ?ThreeGenus ThreeGenus[K] returns the 3-genus of the knot K or a list of the form {lower bound, upper bound}.

In[14]:= ThreeGenus::about The 3-genus program was written by Jake Rasmussen of Princeton University. The program tries to compute the highest nonvanishing group in the knot Floer homology, using Ozsvath and Szabo's version of the Kauffman state model.

The highest 3-genus of the knots known to KnotTheory` is $5$, and there is only one knot with up to 11 crossings whose 3-genus is 5:

In[15]:=	Max[ThreeGenus /@ AllKnots[]]
Out[15]=	5

In[16]:=	Select[AllKnots[], ThreeGenus[#] == 5 &]
Out[16]=	{Knot[11, Alternating, 367]}

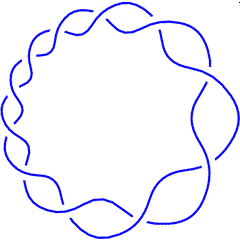K11a367

T(11,2)

(K11a367 is, of couse, also known as the torus knot T(11,2)).

The Conway knot K11n34 is the closure of the braid BR[4, {1, 1, 2, -3, 2, 1, -3, -2, -2, -3, -3}]. Let us compute its 3-genus and compare it with the 3-genus of its mutant companion, the Kinoshita-Terasaka knot K11n42:

In[17]:=	ThreeGenus[BR[4, {1, 1, 2, -3, 2, 1, -3, -2, -2, -3, -3}]]
Out[17]=	3

In[18]:=	ThreeGenus[Knot[11, NonAlternating, 42]]
Out[18]=	2

Bridge Index

The bridge index' of a knot $K$ is the minimal number of local maxima (or local minima) in a generic smooth embedding of $K$ in ${\mathbf {R} }^{3}$.

In[19]:= ?BridgeIndex BridgeIndex[K] returns the bridge index of the knot K, if known to KnotTheory`.

In[20]:= BridgeIndex::about The bridge index data known to KnotTheory` is taken from Charles Livingston's "Table of Knot Invariants", http://www.indiana.edu/~knotinfo/.

An often studied class of knots is the class of 2-bridge knots, knots whose bridge index is 2. Of the 49 prime 9-crossings knots, 24 are 2-bridge:

In[21]:=	Select[AllKnots[], Crossings[#] == 9 && BridgeIndex[#] == 2 &]
Out[21]=	{Knot[9, 1], Knot[9, 2], Knot[9, 3], Knot[9, 4], Knot[9, 5], Knot[9, 6], Knot[9, 7], Knot[9, 8], Knot[9, 9], Knot[9, 10], Knot[9, 11], Knot[9, 12], Knot[9, 13], Knot[9, 14], Knot[9, 15], Knot[9, 17], Knot[9, 18], Knot[9, 19], Knot[9, 20], Knot[9, 21], Knot[9, 23], Knot[9, 26], Knot[9, 27], Knot[9, 31]}

Super Bridge Index

The super bridge index of a knot $K$ is the minimal number, in a generic smooth embedding of $K$ in ${\mathbf {R} }^{3}$, of the maximal number of local maxima (or local minima) in a rigid rotation of that projection.

In[22]:= ?SuperBridgeIndex SuperBridgeIndex[K] returns the super bridge index of the knot K, if known to KnotTheory`. If only a range of possible values is known, a list of the form {min, max} is returned.

In[23]:= SuperBridgeIndex::about The super bridge index data known to KnotTheory` is taken from Charles Livingston's "Table of Knot Invariants", http://www.indiana.edu/~knotinfo/.

Nakanishi Index

In[24]:= ?NakanishiIndex NakanishiIndex[K] returns the Nakanishi index of the knot K, if known to KnotTheory`.

In[25]:= NakanishiIndex::about The Nakanishi index data known to KnotTheory` is taken from Charles Livingston's "Table of Knot Invariants", http://www.indiana.edu/~knotinfo/.

Synthesis

In[26]:=

Profile[K_] := Profile[ SymmetryType[K], UnknottingNumber[K], ThreeGenus[K], BridgeIndex[K], SuperBridgeIndex[K], NakanishiIndex[K] ]

In[27]:=	Profile[Knot[9,24]]
Out[27]=	Profile[Reversible, 1, 3, 3, {4, 6}, 1]

In[28]:=	Ks = Select[AllKnots[], (Crossings[#] == 9 && Profile[#]==Profile[Knot[9,24]])&]
Out[28]=	{Knot[9, 24], Knot[9, 28], Knot[9, 30], Knot[9, 34]}

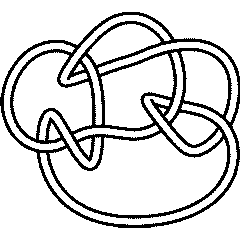9_24

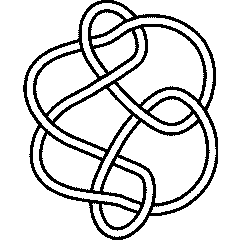9_28

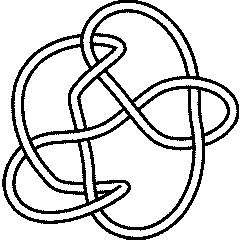9_30

9_34

In[29]:=	Alexander[#][t]& /@ Ks
Out[29]=	-3 5 10 2 3 {13 - t + -- - -- - 10 t + 5 t - t , 2 t t -3 5 12 2 3 -15 + t - -- + -- + 12 t - 5 t + t , 2 t t -3 5 12 2 3 17 - t + -- - -- - 12 t + 5 t - t , 2 t t -3 6 16 2 3 23 - t + -- - -- - 16 t + 6 t - t } 2 t t