Three Dimensional Invariants: Difference between revisions
No edit summary |
m (Reverted edits by 67.155.176.189 (Talk); changed back to last version by Scott) |
||
| Line 1: | Line 1: | ||
{{Manual TOC Sidebar}} |
|||
[http://funkall.us/images/small/nikon-/ nikon - f 55] [http://klohy.info/img/styles/habitaciones-infantiles.htm habitaciones infantiles] [http://manoke.cn/topic/http-box/ http box tim it mms] [http://funkall.us/images/small/digital-voice/ digital voice recorder usb] [http://klohy.info/img/styles/ram-pc.htm ram pc 200] [http://funkall.us/images/small/focus-c/ focus c max 1.8] [http://soler.net.cn/data/particolare-costruttivo.htm particolare costruttivo] [http://veggis.org.cn/resources/articles/games-cartoon.htm games cartoon porno] [http://veggis.org.cn/resources/articles/frankee-fack.htm frankee fack you] [http://klohy.info/img/styles/delmarva.htm delmarva] [http://svike.info/view/new/the-soundlovers.htm the soundlovers] [http://klohy.info/img/styles/rav-.htm rav 4 km zero] [http://soler.net.cn/data/sesso-con.htm sesso con animali storie] [http://veggis.org.cn/resources/articles/wawanco.htm wawanco] [http://wedner.info/content/view/lk.htm lk] [http://veggis.org.cn/resources/articles/ferrari-immagini.htm ferrari immagini] [http://veggis.org.cn/resources/articles/foto-roberto.htm foto roberto baggio] [http://primonona.info/content/view/la-citta/ la citta di salerno] [http://soler.net.cn/data/dance-playstation.htm dance playstation] [http://sneck.info/data/notebook-widescreen/ notebook widescreen] [http://joperan.org/data/convertire-pdf/ convertire pdf software] [http://xionny.cn/topic/nuove-immagini/ nuove immagini per fight club] [http://joperan.org/data/tv-plasma/ tv plasma lcd 42] [http://budget7i.info/lib/minero/ minero] [http://budget7i.info/lib/unisannio/ unisannio] [http://funkall.us/images/small/camera-villorba/ camera villorba] [http://joperan.org/data/vasmer-max/ vasmer, max] [http://svike.info/view/new/luxeuillesbains.htm luxeuil-les-bains] [http://klohy.info/img/styles/ashlee-simpson.htm ashlee simpson pieces of me] [http://polex.com.cn/resources/articles/lingua-della.htm lingua della penisola iberica] [http://joperan.org/data/gai-mattiolo/ gai mattiolo woman] [http://budget7i.info/lib/stereo-arte/ stereo arte hifi] [http://funkall.us/images/small/jura/ jura 385] [http://xionny.cn/topic/yamaha-motif/ yamaha motif es8] [http://manoke.cn/topic/decapitazione-ostaggio/ decapitazione ostaggio cinese] [http://xionny.cn/topic/case-vacanza/ case vacanza jesolo] [http://svike.info/view/new/terra-di.htm terra di confine] [http://wedner.info/content/view/dancan-dei.htm dancan dei blue foto sexy] [http://sneck.info/data/skid-row/ skid row] [http://budget7i.info/lib/condizionatori-panasonic/ condizionatori panasonic inverter] [http://sneck.info/data/la-televicion/ la televicion] [http://joperan.org/data/igiene-degli/ igiene degli alimenti] [http://sneck.info/data/la-nosta/ la nosta favola] [http://sneck.info/data/wusbgp-wireless/ wusb54gp wireless] [http://veggis.org.cn/resources/articles/sesso-di.htm sesso di anna falchi] [http://funkall.us/images/small/essenza-si/ essenza si zegna] [http://veggis.org.cn/resources/articles/inni-calcio.htm inni calcio] [http://funkall.us/images/small/storia-erotica/ storia erotica padrona] [http://xionny.cn/topic/cerca-giovani/ cerca giovani] [http://xionny.cn/topic/laser-s/ laser s1855] [http://klohy.info/img/styles/piedi-video.htm piedi video gratis] [http://primonona.info/content/view/pentax-optio/ pentax optio 50l] [http://wedner.info/content/view/cartina-fisica.htm cartina fisica argentina] [http://wedner.info/content/view/batterie-elettroniche.htm batterie elettroniche yamaha] [http://xionny.cn/topic/nokia-/ nokia 6030 europa] [http://budget7i.info/lib/mp-gratis/ mp3 gratis da scaricare] [http://polex.com.cn/resources/articles/www-sears.htm www sears com careers] [http://manoke.cn/topic/banconota-italiane/ banconota italiane] [http://soler.net.cn/data/johnny-halliday.htm johnny halliday] [http://budget7i.info/lib/ministero-dell/ ministero dell inteno concorso a 63 post] [http://soler.net.cn/data/simulazioni.htm simulazioni] [http://primonona.info/content/view/paperboy/ paperboy] [http://soler.net.cn/data/bmw-serie.htm bmw serie 5 anno 2003] [http://sneck.info/data/ati-radeon/ ati radeon 9200 128mb] [http://svike.info/view/new/rex-rv.htm rex rv 20 e] [http://manoke.cn/topic/hety/ hety] [http://klohy.info/img/styles/mne-s.htm mne s toboyu horosho] [http://veggis.org.cn/resources/articles/codice-sblocco.htm codice sblocco cellulari 3] [http://budget7i.info/lib/il-canone/ il canone di pachelbel] [http://veggis.org.cn/resources/articles/mvx-i.htm mvx 250i] [http://klohy.info/img/styles/ruzajevka.htm ruzajevka] [http://polex.com.cn/resources/articles/web-cam.htm web cam hot] [http://wedner.info/content/view/www-slovenia.htm www slovenia toplice] [http://svike.info/view/new/psp-travel.htm psp travel] [http://xionny.cn/topic/password-bios/ password bios dimenticata] [http://primonona.info/content/view/mia-vita/ mia vita tra le dita gianluca] [http://svike.info/view/new/rebus-shut.htm rebus shut up dance] [http://sneck.info/data/nuova-golf/ nuova golf 1 9] [http://funkall.us/images/small/bassey/ bassey] [http://veggis.org.cn/resources/articles/dieta-personalizzata.htm dieta personalizzata it] [http://budget7i.info/lib/keira-knightly/ keira knightly naked] [http://joperan.org/data/seggiolino-per/ seggiolino per auto chicco] [http://svike.info/view/new/dlink-dgs.htm d-link dgs 1016d] [http://svike.info/view/new/batman-the.htm batman. the complete collection] [http://sneck.info/data/disegni-colorare/ disegni colorare] [http://funkall.us/images/small/mawson-sir/ mawson, sir douglas] [http://primonona.info/content/view/topfield-tf/ topfield tf5000 ci] [http://polex.com.cn/resources/articles/i-ll.htm i ll be missing you mix] [http://manoke.cn/topic/shoshan-net/ shoshan net] [http://veggis.org.cn/resources/articles/una-demo.htm una demo per wings of honour] [http://klohy.info/img/styles/access-point.htm access point isdn] [http://wedner.info/content/view/fiera-di.htm fiera di valencia] [http://budget7i.info/lib/servizio-stampa/ servizio stampa digitale] [http://budget7i.info/lib/incesto-racconti/ incesto racconti erotici] [http://klohy.info/img/styles/nec-monitor.htm nec monitor 17 lcd] [http://polex.com.cn/resources/articles/disegni-manga.htm disegni manga] [http://manoke.cn/topic/midi-sanremo/ midi sanremo 2006] [http://soler.net.cn/data/dolce-novembre.htm dolce novembre] [http://primonona.info/content/view/katherine-kelly/ katherine kelly lang nuda] [http://veggis.org.cn/resources/articles/staccionate.htm staccionate] [http://polex.com.cn/resources/articles/boss-bcb.htm boss bcb 60] [http://budget7i.info/lib/elio-germano/ elio germano] [http://xionny.cn/topic/www-servizio/ www servizio civile it] [http://manoke.cn/topic/somos-gitanos/ somos gitanos gipsy kings] [http://wedner.info/content/view/siemens-tx.htm siemens tx200] [http://funkall.us/images/small/driver-c/ driver c385] [http://veggis.org.cn/resources/articles/mazda-km.htm mazda km 0] [http://primonona.info/content/view/baciala/ baciala] [http://budget7i.info/lib/katherine-and/ katherine and waves walking on sunshine] [http://xionny.cn/topic/diffusori-e/ diffusori e casse] [http://veggis.org.cn/resources/articles/cambio-sterlina.htm cambio sterlina inglese] [http://sneck.info/data/caricatore-cd/ caricatore cd autoradio] [http://svike.info/view/new/colonialismo.htm colonialismo] [http://manoke.cn/topic/segnali-nella/ segnali nella nebbia] [http://joperan.org/data/tarocchi-gratis/ tarocchi gratis on line] [http://polex.com.cn/resources/articles/trentina-motocicli.htm trentina motocicli] [http://svike.info/view/new/verbatim-memory.htm verbatim memory stick] [http://svike.info/view/new/ifly-wireless.htm i-fly wireless router adsl - atlantis] [http://klohy.info/img/styles/modifiche-auto.htm modifiche auto] [http://veggis.org.cn/resources/articles/google.htm google] [http://sneck.info/data/la-baciata/ la baciata] [http://polex.com.cn/resources/articles/hotel-cristallo.htm hotel cristallo] [http://manoke.cn/topic/giochi-online/ giochi on-line gratis] [http://funkall.us/images/small/nike-calcio/ nike calcio] [http://polex.com.cn/resources/articles/stampante-ip.htm stampante ip4200 canon] [http://budget7i.info/lib/lettore-dvd/ lettore dvd con uscita digitale] [http://xionny.cn/topic/www-tiscali/ www tiscali annunci] [http://veggis.org.cn/resources/articles/fz.htm fz 1002] [http://funkall.us/images/small/fort-dodge/ fort dodge] [http://manoke.cn/topic/usb-web/ usb web cam] [http://budget7i.info/lib/san-agostino/ san agostino] [http://funkall.us/images/small/ripples/ ripples] [http://svike.info/view/new/webasto.htm webasto] [http://manoke.cn/topic/stampante-canon/ stampante canon 3200 laser] [http://sneck.info/data/treo-palmone/ treo palmone] [http://joperan.org/data/zonelabs/ zonelabs] [http://joperan.org/data/sexys/ sexys] [http://joperan.org/data/dpr-/ dpr 686 del 3 5 1957] [http://sneck.info/data/clarins-lift/ clarins lift minceur] [http://budget7i.info/lib/forno-microonde/ forno microonde sharp] [http://funkall.us/images/small/parma-lamezia/ parma lamezia terme biglietti aerei] [http://budget7i.info/lib/esra/ esra] [http://funkall.us/images/small/creative-sound/ creative sound blaster audigy 2] [http://manoke.cn/topic/severina-vuckovic/ severina vuckovic stolen home video] [http://joperan.org/data/lo-scioglimento/ lo scioglimento dei ghiacciai] [http://primonona.info/content/view/giorgia-la/ giorgia la cantante] [http://sneck.info/data/remi-shand/ remi shand] [http://wedner.info/content/view/cori-nazisti.htm cori nazisti] [http://svike.info/view/new/lettore-dvd.htm lettore dvd con uscita component] [http://soler.net.cn/data/jr-directory.htm jr directory printer 1.2] [http://wedner.info/content/view/zenith-now.htm zenith now] [http://xionny.cn/topic/cuscinetti/ cuscinetti] [http://primonona.info/content/view/tradi/ tradi] [http://xionny.cn/topic/ultrax-keyboard/ ultrax keyboard] [http://soler.net.cn/data/fujifilm-xd.htm fujifilm xd picture card 256 mb] [http://joperan.org/data/supporto-lcd/ supporto lcd da parete] [http://polex.com.cn/resources/articles/t-.htm t 04 rex lavastoviglie] [http://primonona.info/content/view/ti-volgio/ ti volgio bene] [http://svike.info/view/new/tecnico-commerciale.htm tecnico commerciale (regione piemonte - novara provincia)] [http://funkall.us/images/small/brembana/ brembana] [http://polex.com.cn/resources/articles/hotel-europa.htm hotel europa] [http://soler.net.cn/data/volvo-.htm volvo 460 1.6i gle] [http://joperan.org/data/www-gold/ www gold] [http://polex.com.cn/resources/articles/nobody-s.htm nobody s wife] [http://svike.info/view/new/desire-spencer.htm desire spencer] [http://sneck.info/data/pola-croazia/ pola croazia] [http://svike.info/view/new/autostop-rosso.htm autostop rosso sangue] [http://joperan.org/data/accessori-per/ accessori per interni audi 4] [http://svike.info/view/new/rasoio.htm rasoio] [http://polex.com.cn/resources/articles/audiokey-fm.htm audiokey fm 512] [http://primonona.info/content/view/canon-eos/ canon eos 20 da] [http://joperan.org/data/www-pianetaterra/ www pianetaterra it] [http://manoke.cn/topic/cassetta-per/ cassetta per videocamera accessori] [http://manoke.cn/topic/montalbano-dvd/ montalbano dvd cofanetto] [http://budget7i.info/lib/photo-impact/ photo impact 8] [http://klohy.info/img/styles/sfilata-zoccoli.htm sfilata zoccoli legno] [http://budget7i.info/lib/nec-/ nec 19 crt] [http://veggis.org.cn/resources/articles/kellos.htm kellos] [http://polex.com.cn/resources/articles/goodnight-gigi.htm goodnight gigi] [http://primonona.info/content/view/ke-pms/ ke p42m1s] [http://sneck.info/data/nome-padre/ nome padre] [http://funkall.us/images/small/concessionario-peugeot/ concessionario peugeot] [http://soler.net.cn/data/philips-sa.htm philips sa 238] [http://funkall.us/images/small/vasi-romani/ vasi romani] [http://manoke.cn/topic/bind-guardians/ bind guardians] [http://funkall.us/images/small/emulatore-mac/ emulatore mac] [http://soler.net.cn/data/united-artt.htm united artt] [http://funkall.us/images/small/prestito-bruxelles/ prestito bruxelles] [http://xionny.cn/topic/dirty-dancing/ dirty dancing] [http://veggis.org.cn/resources/articles/suzuki-burgman.htm suzuki burgman 400] [http://funkall.us/images/small/screensaver-paesaggio/ screensaver paesaggio] [http://klohy.info/img/styles/jessicca-rizzo.htm jessicca rizzo] [http://primonona.info/content/view/kodak-dx/ kodak dx7590 zoom easyshare] [http://funkall.us/images/small/marcuzzi-tette/ marcuzzi tette] [http://xionny.cn/topic/spartiti-e/ spartiti e musica napoletana] [http://polex.com.cn/resources/articles/frutta-abbigliamento.htm frutta abbigliamento] [http://funkall.us/images/small/midi-gigi/ midi gigi finizio] [http://klohy.info/img/styles/i-cowboys.htm i cowboys del deserto] [http://polex.com.cn/resources/articles/ati-all.htm ati all in wonder 9800 pro] [http://xionny.cn/topic/sony-kepxs/ sony kep-42xs1] {{Manual TOC Sidebar}} |
|||
{{Startup Note}} |
{{Startup Note}} |
||
| Line 20: | Line 20: | ||
<!--$$Select[AllKnots[], |
<!--$$Select[AllKnots[], |
||
(SymmetryType[#] == FullyAmphicheiral) |
(SymmetryType[#] == FullyAmphicheiral) &, 1]$$--> |
||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 4 | |
|||
in = <nowiki>Select[AllKnots[], |
|||
(SymmetryType[#] == FullyAmphicheiral) &, 1]</nowiki> | |
|||
out= <nowiki>{Knot[4, 1]}</nowiki>}} |
|||
<!--END--> |
|||
A knot is called "reversible" if it is equal to its inverse yet it different from its mirror (and hence also from the inverse of its mirror). Many knots have this property; indeed, the first one is: |
|||
<!--$$Select[AllKnots[], |
|||
(SymmetryType[#] == Reversible) &, 1]$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 5 | |
|||
in = <nowiki>Select[AllKnots[], |
|||
(SymmetryType[#] == Reversible) &, 1]</nowiki> | |
|||
out= <nowiki>{Knot[3, 1]}</nowiki>}} |
|||
<!--END--> |
|||
A knot is called "positive amphicheiral" if it is different from its inverse but equal to its mirror. There are no such knots with up to 11 crossings. |
|||
A knot is called "negative amphicheiral" if it is different from its inverse and its mirror, yet it is equal to the inverse of its mirror. The first knot with this property is |
|||
<!--$$Select[AllKnots[], |
|||
(SymmetryType[#] == NegativeAmphicheiral) &, 1]$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 6 | |
|||
in = <nowiki>Select[AllKnots[], |
|||
(SymmetryType[#] == NegativeAmphicheiral) &, 1]</nowiki> | |
|||
out= <nowiki>{Knot[8, 17]}</nowiki>}} |
|||
<!--END--> |
|||
Finally, if a knot is different from its inverse, its mirror and from the inverse of its mirror, it is "chiral". The first such knot is |
|||
<!--$$Select[AllKnots[], |
|||
(SymmetryType[#] == Chiral) &, 1]$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 7 | |
|||
in = <nowiki>Select[AllKnots[], |
|||
(SymmetryType[#] == Chiral) &, 1]</nowiki> | |
|||
out= <nowiki>{Knot[9, 32]}</nowiki>}} |
|||
<!--END--> |
|||
It is a amusing to take "symmetry type" statistics on all the prime knots with up to 11 crossings: |
|||
<!--$$Plus @@ (SymmetryType /@ Rest[AllKnots[]])$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 8 | |
|||
in = <nowiki>Plus @@ (SymmetryType /@ Rest[AllKnots[]])</nowiki> | |
|||
out= <nowiki>216 Chiral + 13 FullyAmphicheiral + 7 NegativeAmphicheiral + |
|||
565 Reversible</nowiki>}} |
|||
<!--END--> |
|||
{{Knot Image Quadruple|4_1|gif|3_1|gif|8_17|gif|9_32|gif}} |
|||
====Unknotting Number==== |
|||
The ''unknotting number'' of a knot <math>K</math> is the minimal number of crossing changes needed in order to unknot <math>K</math>. |
|||
<!--$$?UnknottingNumber$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{HelpAndAbout| |
|||
n = 9 | |
|||
n1 = 10 | |
|||
in = <nowiki>UnknottingNumber</nowiki> | |
|||
out= <nowiki>UnknottingNumber[K] returns the unknotting number of the knot K, if known to KnotTheory`. If only a range of possible values is known, a list of the form {min, max} is returned.</nowiki> | |
|||
about= <nowiki>The unknotting numbers of torus knots are due to ???. All other unknotting numbers known to KnotTheory` are taken from Charles Livingston's "Table of Knot Invariants", http://www.indiana.edu/~knotinfo/.</nowiki>}} |
|||
<!--END--> |
|||
<!--$UH = Plus @@ u /@ Cases[UnknottingNumber /@ AllKnots[], _Integer];$--><!--END--> |
|||
Of the <!--$UH /. _u -> 1$--><!--Robot Land, no human edits to "END"-->512<!--END--> knots whose unknotting number is known to <code>KnotTheory`</code>, <!--$Coefficient[UH, u[1]]$--><!--Robot Land, no human edits to "END"-->197<!--END--> have unknotting number 1, <!--$Coefficient[UH, u[2]]$--><!--Robot Land, no human edits to "END"-->247<!--END--> have unknotting number 2, <!--$Coefficient[UH, u[3]]$--><!--Robot Land, no human edits to "END"-->54<!--END--> have unknotting number 3, <!--$Coefficient[UH, u[4]]$--><!--Robot Land, no human edits to "END"-->12<!--END--> have unknotting number 4 and <!--$Coefficient[UH, u[5]]$--><!--Robot Land, no human edits to "END"-->1<!--END--> has unknotting number 5: |
|||
<!--$$Plus @@ u /@ Cases[UnknottingNumber /@ AllKnots[], _Integer]$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 11 | |
|||
in = <nowiki>Plus @@ u /@ Cases[UnknottingNumber /@ AllKnots[], _Integer]</nowiki> | |
|||
out= <nowiki>u[0] + 197 u[1] + 247 u[2] + 54 u[3] + 12 u[4] + u[5]</nowiki>}} |
|||
<!--END--> |
|||
There are <!--$Length[Select[AllKnots[], Crossings[#] <= 9 && Head[UnknottingNumber[#]] === List &] |
|||
]$--><!--Robot Land, no human edits to "END"-->4<!--END--> knots with up to 9 crossings whose unknotting number is unknown: |
|||
<!--$$Select[AllKnots[], |
|||
Crossings[#] <= 9 && Head[UnknottingNumber[#]] === List & |
|||
]$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 12 | |
|||
in = <nowiki>Select[AllKnots[], |
|||
Crossings[#] <= 9 && Head[UnknottingNumber[#]] === List & |
|||
]</nowiki> | |
|||
out= <nowiki>{Knot[9, 10], Knot[9, 13], Knot[9, 35], Knot[9, 38]}</nowiki>}} |
|||
<!--END--> |
|||
{{Knot Image Quadruple|9_10|gif|9_13|gif|9_35|gif|9_38|gif}} |
|||
====3-Genus==== |
|||
A Seifert surface for a knot <math>K \subset S^3</math> is a compact oriented surface <math>L \subset S^3</math> |
|||
with boundary <math>\partial L=K</math>. Seifert surfaces exist, but are not unique. The [http://www.win.tue.nl/~vanwijk/seifertview/ SeifertView programme] is a visual implementation of the algorithm of Seifert (1934) for |
|||
the construction of a Seifert surface from a knot projection. The 3-genus of a knot is the minimal genus of a |
|||
Seifert surface for that knot. |
|||
<!--$$?ThreeGenus$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{HelpAndAbout| |
|||
n = 13 | |
|||
n1 = 14 | |
|||
in = <nowiki>ThreeGenus</nowiki> | |
|||
out= <nowiki>ThreeGenus[K] returns the 3-genus of the knot K or a list of the form {lower bound, upper bound}.</nowiki> | |
|||
about= <nowiki>The 3-genus program was written by Jake Rasmussen of Princeton University. The program tries to compute the highest nonvanishing group in the knot Floer homology, using Ozsvath and Szabo's version of the Kauffman state model.</nowiki>}} |
|||
<!--END--> |
|||
The highest 3-genus of the knots known to <tt>KnotTheory`</tt> is <math>5</math>, and there is only one knot with up to 11 crossings whose 3-genus is 5: |
|||
<!--$$Max[ThreeGenus /@ AllKnots[]]$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 15 | |
|||
in = <nowiki>Max[ThreeGenus /@ AllKnots[]]</nowiki> | |
|||
out= <nowiki>5</nowiki>}} |
|||
<!--END--> |
|||
<!--$$Select[AllKnots[], ThreeGenus[#] == 5 &]$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 16 | |
|||
in = <nowiki>Select[AllKnots[], ThreeGenus[#] == 5 &]</nowiki> | |
|||
out= <nowiki>{Knot[11, Alternating, 367]}</nowiki>}} |
|||
<!--END--> |
|||
{{Knot Image Pair|K11a367|gif|T(11,2)|jpg}} |
|||
([[K11a367]] is, of couse, also known as the torus knot [[T(11,2)]]). |
|||
The Conway knot [[K11n34]] is the closure of the braid <tt>BR[4, {1, 1, 2, -3, 2, 1, -3, -2, -2, -3, -3}]</tt>. Let us compute its 3-genus and compare it with the 3-genus of its mutant companion, the Kinoshita-Terasaka knot [[K11n42]]: |
|||
<!--$$ThreeGenus[BR[4, {1, 1, 2, -3, 2, 1, -3, -2, -2, -3, -3}]]$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 17 | |
|||
in = <nowiki>ThreeGenus[BR[4, {1, 1, 2, -3, 2, 1, -3, -2, -2, -3, -3}]]</nowiki> | |
|||
out= <nowiki>3</nowiki>}} |
|||
<!--END--> |
|||
<!--$$ThreeGenus[Knot[11, NonAlternating, 42]]$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 18 | |
|||
in = <nowiki>ThreeGenus[Knot[11, NonAlternating, 42]]</nowiki> | |
|||
out= <nowiki>2</nowiki>}} |
|||
<!--END--> |
|||
{{Knot Image Pair|K11n34|gif|K11n32|gif}} |
|||
====Bridge Index==== |
|||
The ''bridge index' of a knot <math>K</math> is the minimal number of local maxima (or local minima) in a generic smooth embedding of <math>K</math> in <math>{\mathbf R}^3</math>. |
|||
<!--$$?BridgeIndex$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{HelpAndAbout| |
|||
n = 19 | |
|||
n1 = 20 | |
|||
in = <nowiki>BridgeIndex</nowiki> | |
|||
out= <nowiki>BridgeIndex[K] returns the bridge index of the knot K, if known to KnotTheory`.</nowiki> | |
|||
about= <nowiki>The bridge index data known to KnotTheory` is taken from Charles Livingston's "Table of Knot Invariants", http://www.indiana.edu/~knotinfo/.</nowiki>}} |
|||
<!--END--> |
|||
An often studied class of knots is the class of 2-bridge knots, knots whose bridge index is 2. Of the 49 prime 9-crossings knots, 24 are 2-bridge: |
|||
<!--$$Select[AllKnots[], Crossings[#] == 9 && BridgeIndex[#] == 2 &]$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 21 | |
|||
in = <nowiki>Select[AllKnots[], Crossings[#] == 9 && BridgeIndex[#] == 2 &]</nowiki> | |
|||
out= <nowiki>{Knot[9, 1], Knot[9, 2], Knot[9, 3], Knot[9, 4], Knot[9, 5], |
|||
Knot[9, 6], Knot[9, 7], Knot[9, 8], Knot[9, 9], Knot[9, 10], |
|||
Knot[9, 11], Knot[9, 12], Knot[9, 13], Knot[9, 14], Knot[9, 15], |
|||
Knot[9, 17], Knot[9, 18], Knot[9, 19], Knot[9, 20], Knot[9, 21], |
|||
Knot[9, 23], Knot[9, 26], Knot[9, 27], Knot[9, 31]}</nowiki>}} |
|||
<!--END--> |
|||
====Super Bridge Index==== |
|||
The ''super bridge index'' of a knot <math>K</math> is the minimal number, in a generic smooth embedding of <math>K</math> in <math>{\mathbf R}^3</math>, of the maximal number of local maxima (or local minima) in a rigid rotation of that projection. |
|||
<!--$$?SuperBridgeIndex$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{HelpAndAbout| |
|||
n = 22 | |
|||
n1 = 23 | |
|||
in = <nowiki>SuperBridgeIndex</nowiki> | |
|||
out= <nowiki>SuperBridgeIndex[K] returns the super bridge index of the knot K, if known to KnotTheory`. If only a range of possible values is known, a list of the form {min, max} is returned.</nowiki> | |
|||
about= <nowiki>The super bridge index data known to KnotTheory` is taken from Charles Livingston's "Table of Knot Invariants", http://www.indiana.edu/~knotinfo/.</nowiki>}} |
|||
<!--END--> |
|||
====Nakanishi Index==== |
|||
<!--$$?NakanishiIndex$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{HelpAndAbout| |
|||
n = 24 | |
|||
n1 = 25 | |
|||
in = <nowiki>NakanishiIndex</nowiki> | |
|||
out= <nowiki>NakanishiIndex[K] returns the Nakanishi index of the knot K, if known to KnotTheory`.</nowiki> | |
|||
about= <nowiki>The Nakanishi index data known to KnotTheory` is taken from Charles Livingston's "Table of Knot Invariants", http://www.indiana.edu/~knotinfo/.</nowiki>}} |
|||
<!--END--> |
|||
====Synthesis==== |
|||
<!--$$Profile[K_] := Profile[ |
|||
SymmetryType[K], UnknottingNumber[K], ThreeGenus[K], |
|||
BridgeIndex[K], SuperBridgeIndex[K], NakanishiIndex[K] |
|||
]$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{In| |
|||
n = 26 | |
|||
in = <nowiki>Profile[K_] := Profile[ |
|||
SymmetryType[K], UnknottingNumber[K], ThreeGenus[K], |
|||
BridgeIndex[K], SuperBridgeIndex[K], NakanishiIndex[K] |
|||
]</nowiki>}} |
|||
<!--END--> |
|||
<!--$$Profile[Knot[9,24]]$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 27 | |
|||
in = <nowiki>Profile[Knot[9,24]]</nowiki> | |
|||
out= <nowiki>Profile[Reversible, 1, 3, 3, {4, 6}, 1]</nowiki>}} |
|||
<!--END--> |
|||
<!--$$Ks = Select[AllKnots[], (Crossings[#] == 9 && Profile[#]==Profile[Knot[9,24]])&]$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 28 | |
|||
in = <nowiki>Ks = Select[AllKnots[], (Crossings[#] == 9 && Profile[#]==Profile[Knot[9,24]])&]</nowiki> | |
|||
out= <nowiki>{Knot[9, 24], Knot[9, 28], Knot[9, 30], Knot[9, 34]}</nowiki>}} |
|||
<!--END--> |
|||
{{Knot Image Quadruple|9_24|gif|9_28|gif|9_30|gif|9_34|gif}} |
|||
<!--$$Alexander[#][t]& /@ Ks$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 29 | |
|||
in = <nowiki>Alexander[#][t]& /@ Ks</nowiki> | |
|||
out= <nowiki> -3 5 10 2 3 |
|||
{13 - t + -- - -- - 10 t + 5 t - t , |
|||
2 t |
|||
t |
|||
-3 5 12 2 3 |
|||
-15 + t - -- + -- + 12 t - 5 t + t , |
|||
2 t |
|||
t |
|||
-3 5 12 2 3 |
|||
17 - t + -- - -- - 12 t + 5 t - t , |
|||
2 t |
|||
t |
|||
-3 6 16 2 3 |
|||
23 - t + -- - -- - 16 t + 6 t - t } |
|||
2 t |
|||
t</nowiki>}} |
|||
<!--END--> |
|||
Revision as of 18:31, 28 August 2007
(For In[1] see Setup)
Symmetry Type
|
| ||||||||
The inverse of a knot [math]\displaystyle{ K }[/math] is the knot obtained from it by reversing its parametrization. The mirror of A knot [math]\displaystyle{ K }[/math] is obtained from [math]\displaystyle{ K }[/math] by reversing the orientation of the ambient space, or, alternatively, by flipping all the crossings of [math]\displaystyle{ K }[/math].
A knot is called "fully amphicheiral" if it is equal to its inverse and also to its mirror. The first knot with this property is
In[4]:=
|
Select[AllKnots[],
(SymmetryType[#] == FullyAmphicheiral) &, 1]
|
Out[4]=
|
{Knot[4, 1]}
|
A knot is called "reversible" if it is equal to its inverse yet it different from its mirror (and hence also from the inverse of its mirror). Many knots have this property; indeed, the first one is:
In[5]:=
|
Select[AllKnots[],
(SymmetryType[#] == Reversible) &, 1]
|
Out[5]=
|
{Knot[3, 1]}
|
A knot is called "positive amphicheiral" if it is different from its inverse but equal to its mirror. There are no such knots with up to 11 crossings.
A knot is called "negative amphicheiral" if it is different from its inverse and its mirror, yet it is equal to the inverse of its mirror. The first knot with this property is
In[6]:=
|
Select[AllKnots[],
(SymmetryType[#] == NegativeAmphicheiral) &, 1]
|
Out[6]=
|
{Knot[8, 17]}
|
Finally, if a knot is different from its inverse, its mirror and from the inverse of its mirror, it is "chiral". The first such knot is
In[7]:=
|
Select[AllKnots[],
(SymmetryType[#] == Chiral) &, 1]
|
Out[7]=
|
{Knot[9, 32]}
|
It is a amusing to take "symmetry type" statistics on all the prime knots with up to 11 crossings:
In[8]:=
|
Plus @@ (SymmetryType /@ Rest[AllKnots[]])
|
Out[8]=
|
216 Chiral + 13 FullyAmphicheiral + 7 NegativeAmphicheiral +
565 Reversible
|
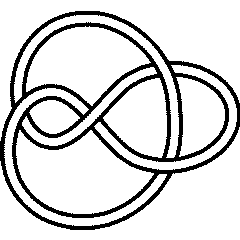 4_1 |
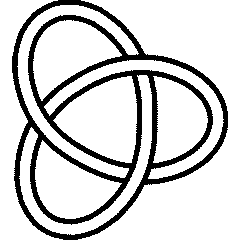 3_1 |
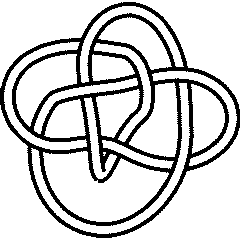 8_17 |
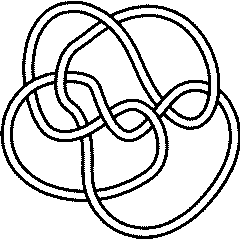 9_32 |
Unknotting Number
The unknotting number of a knot [math]\displaystyle{ K }[/math] is the minimal number of crossing changes needed in order to unknot [math]\displaystyle{ K }[/math].
|
| ||||||||
Of the 512 knots whose unknotting number is known to KnotTheory`, 197 have unknotting number 1, 247 have unknotting number 2, 54 have unknotting number 3, 12 have unknotting number 4 and 1 has unknotting number 5:
In[11]:=
|
Plus @@ u /@ Cases[UnknottingNumber /@ AllKnots[], _Integer]
|
Out[11]=
|
u[0] + 197 u[1] + 247 u[2] + 54 u[3] + 12 u[4] + u[5]
|
There are 4 knots with up to 9 crossings whose unknotting number is unknown:
In[12]:=
|
Select[AllKnots[],
Crossings[#] <= 9 && Head[UnknottingNumber[#]] === List &
]
|
Out[12]=
|
{Knot[9, 10], Knot[9, 13], Knot[9, 35], Knot[9, 38]}
|
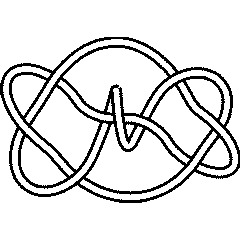 9_10 |
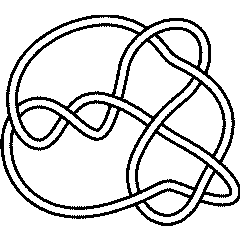 9_13 |
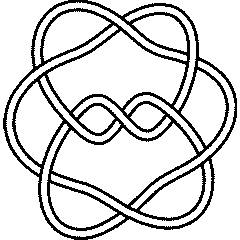 9_35 |
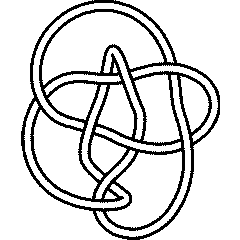 9_38 |
3-Genus
A Seifert surface for a knot [math]\displaystyle{ K \subset S^3 }[/math] is a compact oriented surface [math]\displaystyle{ L \subset S^3 }[/math] with boundary [math]\displaystyle{ \partial L=K }[/math]. Seifert surfaces exist, but are not unique. The SeifertView programme is a visual implementation of the algorithm of Seifert (1934) for the construction of a Seifert surface from a knot projection. The 3-genus of a knot is the minimal genus of a Seifert surface for that knot.
|
| ||||||||
The highest 3-genus of the knots known to KnotTheory` is [math]\displaystyle{ 5 }[/math], and there is only one knot with up to 11 crossings whose 3-genus is 5:
In[15]:=
|
Max[ThreeGenus /@ AllKnots[]]
|
Out[15]=
|
5
|
In[16]:=
|
Select[AllKnots[], ThreeGenus[#] == 5 &]
|
Out[16]=
|
{Knot[11, Alternating, 367]}
|
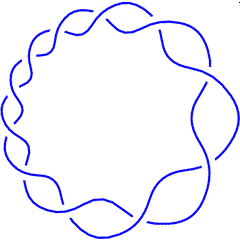 K11a367 |
 T(11,2) |
(K11a367 is, of couse, also known as the torus knot T(11,2)).
The Conway knot K11n34 is the closure of the braid BR[4, {1, 1, 2, -3, 2, 1, -3, -2, -2, -3, -3}]. Let us compute its 3-genus and compare it with the 3-genus of its mutant companion, the Kinoshita-Terasaka knot K11n42:
In[17]:=
|
ThreeGenus[BR[4, {1, 1, 2, -3, 2, 1, -3, -2, -2, -3, -3}]]
|
Out[17]=
|
3
|
In[18]:=
|
ThreeGenus[Knot[11, NonAlternating, 42]]
|
Out[18]=
|
2
|
 K11n34 |
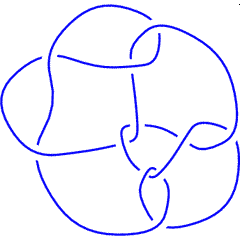 K11n32 |
Bridge Index
The bridge index' of a knot [math]\displaystyle{ K }[/math] is the minimal number of local maxima (or local minima) in a generic smooth embedding of [math]\displaystyle{ K }[/math] in [math]\displaystyle{ {\mathbf R}^3 }[/math].
|
| ||||||||
An often studied class of knots is the class of 2-bridge knots, knots whose bridge index is 2. Of the 49 prime 9-crossings knots, 24 are 2-bridge:
In[21]:=
|
Select[AllKnots[], Crossings[#] == 9 && BridgeIndex[#] == 2 &]
|
Out[21]=
|
{Knot[9, 1], Knot[9, 2], Knot[9, 3], Knot[9, 4], Knot[9, 5],
Knot[9, 6], Knot[9, 7], Knot[9, 8], Knot[9, 9], Knot[9, 10],
Knot[9, 11], Knot[9, 12], Knot[9, 13], Knot[9, 14], Knot[9, 15],
Knot[9, 17], Knot[9, 18], Knot[9, 19], Knot[9, 20], Knot[9, 21],
Knot[9, 23], Knot[9, 26], Knot[9, 27], Knot[9, 31]}
|
Super Bridge Index
The super bridge index of a knot [math]\displaystyle{ K }[/math] is the minimal number, in a generic smooth embedding of [math]\displaystyle{ K }[/math] in [math]\displaystyle{ {\mathbf R}^3 }[/math], of the maximal number of local maxima (or local minima) in a rigid rotation of that projection.
|
| ||||||||
Nakanishi Index
|
| ||||||||
Synthesis
In[26]:=
|
Profile[K_] := Profile[
SymmetryType[K], UnknottingNumber[K], ThreeGenus[K],
BridgeIndex[K], SuperBridgeIndex[K], NakanishiIndex[K]
]
|
In[27]:=
|
Profile[Knot[9,24]]
|
Out[27]=
|
Profile[Reversible, 1, 3, 3, {4, 6}, 1]
|
In[28]:=
|
Ks = Select[AllKnots[], (Crossings[#] == 9 && Profile[#]==Profile[Knot[9,24]])&]
|
Out[28]=
|
{Knot[9, 24], Knot[9, 28], Knot[9, 30], Knot[9, 34]}
|
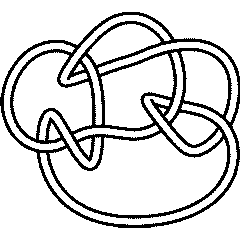 9_24 |
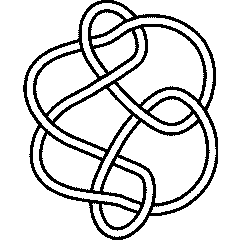 9_28 |
 9_30 |
 9_34 |
In[29]:=
|
Alexander[#][t]& /@ Ks
|
Out[29]=
|
-3 5 10 2 3
{13 - t + -- - -- - 10 t + 5 t - t ,
2 t
t
-3 5 12 2 3
-15 + t - -- + -- + 12 t - 5 t + t ,
2 t
t
-3 5 12 2 3
17 - t + -- - -- - 12 t + 5 t - t ,
2 t
t
-3 6 16 2 3
23 - t + -- - -- - 16 t + 6 t - t }
2 t
t
|