Printable Manual: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
<!-- |
<!-- Warning! It's important that we keep this page synchronised with [[Manual Table of Contents]]. --> |
||
<!-- If you've added something there, make sure to make the corresponding change here. --> |
|||
<!-- Entries on [[Manual Table of Contents]] which point to a section of a page should *not* be listed here, --> |
|||
<!-- because that section will have already been transcluded as part of its containing page. --> |
|||
<!-- The levels indicated by * and ** on [[Manual Table of Contents]] are reflected here by the heading level below. --> |
|||
<!-- For example, |
|||
<!-- * [[Presentations]] |
|||
| ⚫ | |||
Becomes |
|||
==Presentations== |
|||
{{:Presentations}} |
|||
===Planar Diagrams=== |
|||
{{:Planar Diagrams}} |
|||
in the page below. |
|||
--> |
|||
Return to the wiki [[The Mathematica Package KnotTheory`|manual]]. |
Return to the wiki [[The Mathematica Package KnotTheory`|manual]]. |
||
| Line 15: | Line 28: | ||
===Gauss Codes=== |
===Gauss Codes=== |
||
{{:Gauss Codes}} |
{{:Gauss Codes}} |
||
===DT (Dowker-Thistlethwaite) Codes=== |
|||
{{:DT (Dowker-Thistlethwaite) Codes}} |
|||
| ⚫ | |||
===Braid Representatives=== |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
*** [[Drawing Planar Diagrams#How does it work?|How does it work?]] |
|||
{{:Graphical Output}} |
|||
| ⚫ | |||
===Drawing Planar Diagrams=== |
|||
| ⚫ | |||
{{:Drawing Planar Diagrams}} |
|||
| ⚫ | |||
===Drawing Braids=== |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
{{:Structure and Operations}} |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
{{:Invariants}} |
|||
*** [[The Jones Polynomial#How is the Jones polynomial computed?|How is the Jones polynomial computed?]] |
|||
===Invariants from Braid Theory=== |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
===Three Dimensional Invariants=== |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
===The Alexander-Conway Polynomial=== |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
===The Determinant and the Signature=== |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
===The Jones Polynomial=== |
|||
*** [[Drawing with TubePlot#Standalone TubePlot|Standalone TubePlot]] |
|||
| ⚫ | |||
| ⚫ | |||
===The Coloured Jones Polynomials=== |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
===The A2 Invariant=== |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
===The HOMFLY-PT Polynomial=== |
|||
** [[Further Knot Theory Software#Knotscape|Knotscape]] |
|||
| ⚫ | |||
| ⚫ | |||
===The Kauffman Polynomial=== |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
===Finite Type (Vassiliev) Invariants=== |
|||
| ⚫ | |||
===Khovanov Homology=== |
|||
| ⚫ | |||
| ⚫ | |||
{{:Extras Included with KnotTheory`}} |
|||
===Drawing with TubePlot=== |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
{{:Lightly Documented Features}} |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
{{:How to Edit this Manual...}} |
|||
| ⚫ | |||
{{:About this Manual...}} |
|||
| ⚫ | |||
{{:Bibliography}} |
|||
Revision as of 12:05, 29 August 2005
Return to the wiki manual.
Acknowledgement
This Atlas is partially (and indirectly) supported by NSERC grant RGPIN 262178. As a Wiki project, it doesn't make sense anymore to acknowledge individual contributors. Yet for historical purposes, here's our acknowledgement as of the conversion to Wiki formnat on August 2005:
- Jana Archibald, for writing the program
Alexander[K, r]. - Sergei Chmutov, for spotting a typo.
- David De Wit, for a bug report.
- Ralph Furmaniak, for help with our link to Knotilus (see Gauss Codes).
- Stavros Garoufalidis, for jointly writing the program ColouredJones (see The Coloured Jones Polynomials).
- Thomas Gittings, for the minimum braid representatives for the knots with up to 10 crossings (see Braid Representatives).
- Jeremy Green, for his java implementation of
Kh(see Khovanov Homology). - Thang Le, for supplying some of the formulas used in the program ColouredJones (see The Coloured Jones Polynomials).
- Rick Litherland, for spotting a sneaky bug in the program
KnotSignature. - Charles Livingston, for allowing us to bundle data from his Table of Knot Invariants.
- Scott Morrison, for a bug report and for writing the programs to compute the HOMFLY-PT and Kauffman polynomials (see The HOMFLY-PT Polynomial and The Kauffman Polynomial).
- Bertrand Patureau-Mirand, for informing us of some mismatches in the link tables (now corrected).
- Jozef Przytycki, for correcting a typo.
- Stuart Rankin, for help with our link to Knotilus (see Gauss Codes).
- Emily Redelmeier, for writing the program DrawPD (see Drawing Planar Diagrams).
- Siddarth Sankaran, for writing the conversion program between Gauss codes and PD codes and for writing MorseLink and DrawMorseLink.
- Alexander Shumakovitch, for his help with signature computations (see The Determinant and the Signature).
- Alexander Stoimenow, for the knot presentations for the knots in the Rolfsen table and some further remarks.
- Z-X. Tao, for noticing problems with the knots 10_83 and 10_86.
- Morwen Thistlethwaite, for the pictures of links and of 11 crossing knots.
- Dylan Thurston, for writing an early routine to translate from Hoste-Thistlethwaite's DT codes to my "PD Presentations".
Setup
Start by downloading the file KnotTheory.zip (around 15MB), and unpack it. This will create a subdirectory KnotTheory/ in your current working directory. This done, no installation is required (though you may wish to check out Further Data Files and/or Setting the Path below). Start Mathematica and you're ready to go:
In[2]:= << KnotTheory`
Loading KnotTheory` version of March 22, 2011, 21:10:4.67737. Read more at http://katlas.org/wiki/KnotTheory.
Notice the little "prime" at the end of KnotTheory above. It is a backquote (find it on the upper left side of most keyboards) and not a quote, and it really has to be there for things to work.
Let us check that everything is working well:
In[3]:=
|
Alexander[Knot[6, 2]][t]
|
Out[3]=
|
-2 3 2
-3 - t + - + 3 t - t
t
|
| ||||
| ||||
| ||||
Thus on the day this manual page was last changed, we had:
In[7]:=
|
{KnotTheoryVersion[], KnotTheoryVersionString[]}
|
Out[7]=
|
{{2011, 3, 22, 21, 10, 4.67737}, March 22, 2011, 21:10:4.67737}
|
In[8]:=
|
KnotTheoryWelcomeMessage[]
|
Out[8]=
|
Loading KnotTheory` version of March 22, 2011, 21:10:4.67737.
Read more at http://katlas.org/wiki/KnotTheory.
|
| ||||
In[10]:=
|
KnotTheoryDirectory[]
|
Out[10]=
|
C:\Documents and Settings\pc\Documenti\Wolfram\KnotTheory
|
KnotTheoryDirectory may not work under some operating systems/environments. Please let Dror know if you encounter any difficulties.
Notes
Precomputed Data
KnotTheory` comes with a certain amount of precomputed data which is loaded "on demand" just when it is needed. When a precomputed data file is read by KnotTheory`, a notification message is displayed. To prevent these messages from appearing execute the command Off[KnotTheory::loading].
Further Data Files
To access the Hoste-Thistlethwaite enumeration of knots with 12 to 16 crossings (see Naming and Enumeration), also download either the file DTCodes4Knots12To16.tar.gz or the file DTCodes4Knots12To16.zip (about 9MB each), and unpack either one into the directory KnotTheory/.
Setting the Path
The directions above are written on the assumption that the package KnotTheory` (more precisely, the directory KnotTheory/ containing the files that make this package), is somewhere on your Mathematica search path. Usually this will be the case if KnotTheory/ is a subdirectory of your current working directory. If for some reason Mathematica cannot find KnotTheory`, you may tell it where to look in either of the following three ways. Assume KnotTheory/ is a subdirectory of FullPathToKnotTheory:
- If you are using KnotTheory` rarely and you don't want to change system defaults, evaluate AppendTo[$Path,"FullPathToKnotTheory"] within Mathematica before attempting to load KnotTheory`.
- If you plan to use KnotTheory` often, you may want to move the directory KnotTheory/ into one of the directories on your path. Evaluate $Path within Mathematica to see what those are.
- Alternatively, you may permanently add FullPathToKnotTheory to your $Path. To do that, find your Mathematica base directory by evaluating $UserBaseDirectory (on Dror's laptop, this comes out to be C:\Users\Dror\AppData\Roaming\Mathematica), and then add the line AppendTo[$Path,"FullPathToKnotTheory/"] to the file $BaseDirectory/Kernel/init.m and restart Mathematica.
Naming and Enumeration
KnotTheory` comes loaded with some knot tables; currently, the Rolfsen table of prime knots with up to 10 crossings [Rolfsen], the Hoste-Thistlethwaite tables of prime knots with up to 16 crossings and the Thistlethwaite table of prime links with up to 11 crossings (see Knotscape):
(For In[1] see Setup)
| ||||
| ||||
 6_1 |
 9_46 |
Thus, for example, let us verify that the knots 6_1 and 9_46 have the same Alexander polynomial:
In[4]:=
|
Alexander[Knot[6, 1]][t]
|
Out[4]=
|
2
5 - - - 2 t
t
|
In[5]:=
|
Alexander[Knot[9, 46]][t]
|
Out[5]=
|
2
5 - - - 2 t
t
|
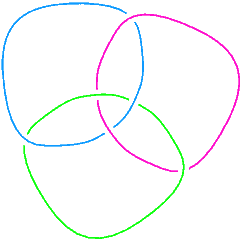 L6a4 |
We can also check that the Borromean rings, L6a4 in the Thistlethwaite table, is a 3-component link:
In[6]:=
|
Length[Skeleton[Link[6, Alternating, 4]]]
|
Out[6]=
|
3
|
| ||||
| ||||
Thus at the moment there are 1701936 knots and 5700 links known to KnotTheory`:
In[9]:=
|
Length /@ {AllKnots[{0,16}], AllLinks[{2,12}]}
|
Out[9]=
|
{1701936, 5700}
|
In[10]:=
|
Show[DrawPD[Knot[13, NonAlternating, 5016], {Gap -> 0.025}]]
|
| |
Out[10]=
|
-Graphics-
|
(Shumakovitch had noticed that this nice knot has interesting Khovanov homology; see [Shumakovitch]).
 T(5,3) |
In addition to the tables, KnotTheory` also knows about torus knots:
| ||||
| ||||
For example, the torus knots T(5,3) and T(3,5) have different presentations with different numbers of crossings, but they are in fact isotopic, and hence they have the same invariants (and in particular the same type 3 Vassiliev invariant ):
In[13]:=
|
Crossings /@ {TorusKnot[5, 3], TorusKnot[3, 5]}
|
Out[13]=
|
{10, 12}
|
In[14]:=
|
Vassiliev[3] /@ {TorusKnot[5, 3], TorusKnot[3, 5]}
|
Out[14]=
|
{20, 20}
|
KnotTheory` knows how to plot torus knots; see Drawing with TubePlot.
You can also use the function Knot to parse certain string representations of named knots:
In[15]:=
|
Knot /@ {"K11a14", "11a_14", "L8a1", "T(3,5)"}
|
Out[15]=
|
{Knot[11, Alternating, 14], If[11 a <= 10 &&
14 <= NumberOfKnots[11 a, Alternating] +
NumberOfKnots[11 a, NonAlternating],
Knot @@ KnotTheory`Naming`s$3008], Link[8, Alternating, 1],
TorusKnot[3, 5]}
|
In the opposite direction, the function NameString produces the standard name for a knot, used throughout the Knot Atlas.
In[16]:=
|
NameString /@ {Knot[11, Alternating, 14], TorusKnot[3,5]}
|
Out[16]=
|
{K11a14, T(3,5)}
|
References
[Rolfsen] ^ D. Rolfsen, Knots and Links, Publish or Perish, Mathematics Lecture Series 7, Wilmington 1976.
[Shumakovitch] ^ A. Shumakovitch, Torsion of the Khovanov Homology, arXiv:math.GT/0405474.
Presentations
KnotTheory` uses several presentations for knots/links.
- Planar Diagrams
- Gauss Codes
- DT (Dowker-Thistlethwaite) Codes
- Braid Representatives
- MorseLink Presentations
- Arc Presentations
- Conway Notation
Planar Diagrams
In the "Planar Diagrams" (PD) presentation we present every knot or link diagram by labeling its edges (with natural numbers, 1,...,n, and with increasing labels as we go around each component) and by a list crossings presented as symbols where , , and are the labels of the edges around that crossing, starting from the incoming lower edge and proceeding counterclockwise. Thus for example, the PD presentation of the knot above is:
(This of course is the Miller Institute knot, the mirror image of the knot 6_2)
(For In[1] see Setup)
|
| ||||||||
| ||||
Thus, for example, let us compute the determinant of the above knot:
In[5]:=
|
K = PD[
X[1,9,2,8], X[3,10,4,11], X[5,3,6,2],
X[7,1,8,12], X[9,4,10,5], X[11,7,12,6]
];
|
In[6]:=
|
Alexander[K][-1]
|
Out[6]=
|
-11
|
Some further details
| ||||
| ||||
| ||||
For example, we could add an extra "point" on the Miller Institute knot, splitting edge 12 into two pieces, labeled 12 and 13:
In[10]:=
|
K1 = PD[
X[1,9,2,8], X[3,10,4,11], X[5,3,6,2],
X[7,1,8,13], X[9,4,10,5], X[11,7,12,6],
P[12,13]
];
|
At the moment, many of our routines do not know to ignore such "extra points". But some do:
In[11]:=
|
Jones[K][q] == Jones[K1][q]
|
Out[11]=
|
True
|
| ||||
Hence we can verify that the A2 invariant of the unknot is :
In[13]:=
|
A2Invariant[Loop[1]][q]
|
Out[13]=
|
-2 2
1 + q + q
|
Gauss Codes
The Gauss Code of an -crossing knot or link is obtained as follows:
- Number the crossings of from 1 to in an arbitrary manner.
- Order the components of is some arbitrary manner.
- Start "walking" along the first component of , taking note of the numbers of the crossings you've gone through. If in a given crossing you cross on the "over" strand, write down the number of that crossing. If you cross on the "under" strand, write down the negative of the number of that crossing.
- Do the same for all other components of (if any).
The resulting list of signed integers (in the case of a knot) or list of lists of signed integers (in the case of a link) is called the Gauss Code of . KnotTheory` has some rudimentary support for Gauss codes:
(For In[1] see Setup)
| ||||
Thus for example, the Gauss codes for the trefoil knot and the Borromean link are:
In[3]:=
|
GaussCode /@ {Knot[3, 1], Link[6, Alternating, 4]}
|
Out[3]=
|
{GaussCode[-1, 3, -2, 1, -3, 2],
GaussCode[{1, -6, 5, -3}, {4, -1, 2, -5}, {6, -4, 3, -2}]}
|
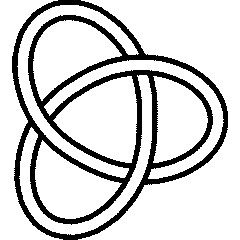 3_1 |
 L6a4 |
Ralph Furmaniak, working under the guidance of Stuart Rankin and Ortho Flint at the University of Western Ontario, wrote a web-based server called "Knotilus" that takes Gauss codes and outputs pictures of the desired knots and links in several standard image formats.
| ||||
Thus,
In[5]:=
|
KnotilusURL /@ {Knot[3, 1], Link[6, Alternating, 4]}
|
Out[5]=
|
{http://srankin.math.uwo.ca/cgi-bin/retrieve.cgi/-1,3,-2,1,-3,2/goTop.h\
tml, http://srankin.math.uwo.ca/cgi-bin/retrieve.cgi/1,-6,5,-3:4,-1,\
2,-5:6,-4,3,-2/goTop.html}
|
DT (Dowker-Thistlethwaite) Codes
Knots
The "DT Code" ("DT" after Clifford Hugh Dowker and Morwen Thistlethwaite) of a knot is obtained as follows:
- Start "walking" along and count every crossing you pass through. If has crossings and given that every crossing is visited twice, the count ends at . Label each crossing with the values of the counter when it is visited, though when labeling by an even number, take it with a minus sign if you are walking "over" the crossing.
- Every crossing is now labeled with two integers whose absolute values run from to . It is easy to see that each crossing is labeled with one odd integer and one even integer. The DT code of is the list of even integers paired with the odd integers 1, 3, 5, ..., taken in this order. Thus for example the pairing for the knot in the figure below is , and hence its DT code is (and as DT codes are insensitive to overall mirrors, this is equivalent to ).
KnotTheory` has some rudimentary support for DT codes:
(For In[1] see Setup)
| ||||
Thus for example, the DT codes for the last 9 crossing alternating knot 9_41 and the first 9 crossing non alternating knot 9_42 are:
In[3]:=
|
dts = DTCode /@ {Knot[9, 41], Knot[9, 42]}
|
Out[3]=
|
{DTCode[6, 10, 14, 12, 16, 2, 18, 4, 8],
DTCode[4, 8, 10, -14, 2, -16, -18, -6, -12]}
|
(The DT code of an alternating knot is always a sequence of positive numbers but the DT code of a non alternating knot contains both signs.)
 9_41 |
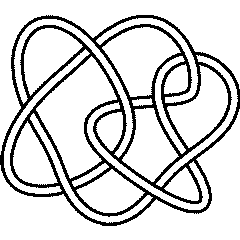 9_42 |
DT codes and Gauss codes carry the same information and are easily convertible:
In[4]:=
|
gcs = GaussCode /@ dts
|
Out[4]=
|
{GaussCode[1, -6, 2, -8, 3, -1, 4, -9, 5, -2, 6, -4, 7, -3, 8, -5, 9,
-7], GaussCode[1, -5, 2, -1, 3, 8, -4, -2, 5, -3, -6, 9, -7, 4, -8,
6, -9, 7]}
|
In[5]:=
|
DTCode /@ gcs
|
Out[5]=
|
{DTCode[6, 10, 14, 12, 16, 2, 18, 4, 8],
DTCode[4, 8, 10, -14, 2, -16, -18, -6, -12]}
|
Conversion between DT codes and/or Gauss codes and PD codes is more complicated; the harder side, going from DT/Gauss to PD, was written by Siddarth Sankaran at the University of Toronto:
In[6]:=
|
PD[DTCode[4, 6, 2]]
|
Out[6]=
|
PD[X[4, 2, 5, 1], X[6, 4, 1, 3], X[2, 6, 3, 5]]
|
Links
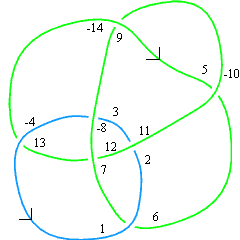
DT Codes for links are defined in a similar way (see [DollHoste]). Follow the same numbering process as for knots, except when you finish traversing one component, jump straight to the next. It is not difficult to see that there is always a choice of starting points along the components for which the resulting pairing is a pairing between odd and even numbers. (On the figure above one possible choice is indicated). Again, it is enough to only list the even numbers corresponding to ; call the resulting list . (Above, ). Notice that the odd indices are naturally subdivided into sublists according to the component of the link on which they lie, and this induces a subdivision of into sublists. Thus with the choices made in the figure above, the DT code for the link L7n2 is .
KnotTheory` knows about DT codes for links:
In[7]:=
|
DTCode[Link[7, NonAlternating, 2]]
|
Out[7]=
|
DTCode[{6, -8}, {-10, 12, -14, 2, -4}]
|
In[8]:=
|
MultivariableAlexander[DTCode[{6, -8}, {-10, 12, -14, 2, -4}]][t]
|
Out[8]=
|
(-1 + t[1]) (-1 + t[2])
-----------------------
Sqrt[t[1]] Sqrt[t[2]]
|
[DollHoste] ^ H. Doll and J. Hoste, A tabulation of oriented links, Mathematics of Computation 57-196 (1991) 747-761.
Braid Representatives
Every knot and every link is the closure of a braid. KnotTheory` can also represent knots and links as braid closures:
(For In[1] see Setup)
|
| ||||||||
| ||||
Thus for example,
In[5]:=
|
br1 = BR[2, {-1, -1, -1}];
|
In[6]:=
|
PD[br1]
|
Out[6]=
|
PD[X[6, 3, 1, 4], X[4, 1, 5, 2], X[2, 5, 3, 6]]
|
In[7]:=
|
Jones[br1][q]
|
Out[7]=
|
-4 -3 1
-q + q + -
q
|
In[8]:=
|
Mirror[br1]
|
Out[8]=
|
BR[2, {1, 1, 1}]
|
 T(5,4) |
 K11a362 |
KnotTheory` has the braid representatives of some knots and links pre-loaded, and for all other knots and links it will find a braid representative using Vogel's algorithm. Thus for example,
In[9]:=
|
BR[TorusKnot[5, 4]]
|
Out[9]=
|
BR[4, {1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3}]
|
In[10]:=
|
BR[Knot[11, Alternating, 362]]
|
Out[10]=
|
BR[10, {1, 2, -3, -4, 5, 6, 5, 4, 3, -2, -1, -4, 3, -2, -4, 3, 5, 4,
-6, 7, -6, 5, 8, 7, 6, 5, -4, -3, 2, 5, -6, 9, -8, 7, -6, 5, 4, -3,
5, 6, 5, 4, 5, -7, 8, -7, 6, 5, -9, -8, -7}]
|
(As we see, Vogel's algorithm sometimes produces scary results. A 51-crossings braid representative for an 11-crossing knot, in the case of K11a362).
 10_1 |
 5_2 |
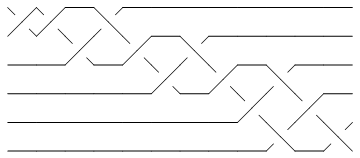
The minimum braid representative of a given knot is a braid representative for that knot which has a minimal number of braid crossings and within those braid representatives with a minimal number of braid crossings, it has a minimal number of strands (full details are in [Gittings]). Thomas Gittings kindly provided us the minimum braid representatives for all knots with up to 10 crossings. Thus for example, the minimum braid representative for the knot 10_1 has length (number of crossings) 13 and width 6 (number of strands, also see Invariants from Braid Theory):
In[11]:=
|
br2 = BR[Knot[10, 1]]
|
Out[11]=
|
BR[6, {-1, -1, -2, 1, -2, -3, 2, -3, -4, 3, 5, -4, 5}]
|
In[12]:=
|
Show[BraidPlot[CollapseBraid[br2]]]
|
| |
Out[12]=
|
-Graphics-
|
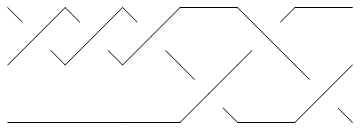
Already for the knot 5_2 the minimum braid is shorter than the braid produced by Vogel's algorithm. Indeed, the minimum braid is
In[13]:=
|
Show[BraidPlot[CollapseBraid[BR[Knot[5, 2]]]]]
|
| |
Out[13]=
|
-Graphics-
|
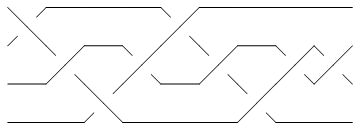
To force KnotTheory` to run Vogel's algorithm on 5_2, we first convert it to its PD form,
In[14]:=
|
pd = PD[Knot[5, 2]]
|
Out[14]=
|
PD[X[1, 4, 2, 5], X[3, 8, 4, 9], X[5, 10, 6, 1], X[9, 6, 10, 7],
X[7, 2, 8, 3]]
|
and only then run BR:
In[15]:=
|
Show[BraidPlot[CollapseBraid[BR[pd]]]]
|
| |
Out[15]=
|
-Graphics-
|
(Check Drawing Braids for information about the command BraidPlot and the related command CollapseBraid.)
[Gittings] ^ T. A. Gittings, Minimum braids: a complete invariant of knots and links, arXiv:math.GT/0401051.
Graphical Output
KnotTheory` can draw knots and links in several ways.
Drawing Planar Diagrams
My summer student Emily Redelmeier is in the process of writing a program that uses circle packing to draw an arbitrary object given as a PD as in Planar Diagrams. At the moment her program is still slow, limited and sometimes buggy, but it is already quite useful, as the following lines show:
(For In[1] see Setup)
|
| ||||||||
Thus, for example, here's the torus knot T(4,3):
In[4]:=
|
Show[DrawPD[TorusKnot[4, 3]]]
|
| |
Out[4]=
|
-Graphics-
|
One problem we currently have is that crossings come out at non-uniform sizes, hence in the picture below you may need magnifying glasses to decide who's over and who's under:
In[5]:=
|
MillettUnknot = PD[
X[1,10,2,11], X[9,2,10,3], X[3,7,4,6], X[15,5,16,4],
X[5,17,6,16],X[7,14,8,15], X[8,18,9,17], X[11,18,12,19],
X[19,12,20,13], X[13,20,14,1]
];
|
In[6]:=
|
Show[DrawPD[MillettUnknot]]
|
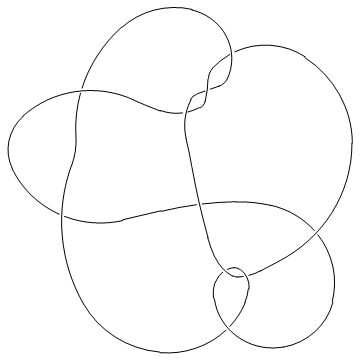
| |
Out[6]=
|
-Graphics-
|
In such a situation, the option Gap is sometimes handy:
In[7]:=
|
Show[DrawPD[MillettUnknot, {Gap -> 0.03}]]
|
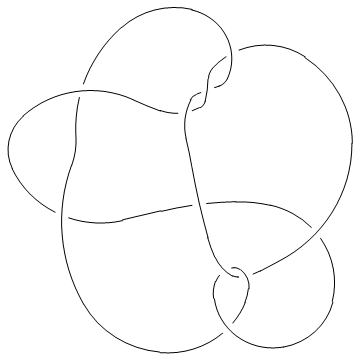
| |
Out[7]=
|
-Graphics-
|
How does it work?
DrawPD uses Andreev's theorem [Andreev1], [Andreev2], which states that every planar graph can be realized, nearly uniquely, as the graph of tangencies of circles drawn within the unit disk. That is, to every vertex of one may associate a disk within the unit disk, so that the interiors of these disks are disjoint and they are tangent iff the corresponding vertices are connected by an edge. The Andreev "circle packing" corresponding to the knot 4_1 is the first picture on the right (circle 13 is the unit disk itself).
But now every ingredient of the original knot (every arc, crossing and face) has a disk in the plane in which it can be cleanly drawn and clashes are guaranteed not to occur. Furthermore, knowing the precise coordinates of all the tangency points allows us to represent each ingredient by some nice smooth arcs that meet smoothly. The result is the second picture on the right. Removing all the circles, what remains is the desired clean planar picture of 4_1.
[Andreev1] ^ A. Andreev, On convex polyhedra in Lobacevskii spaces (in Russian), Math. Sbornik USSR, Nov. Ser. 81 (1970) 445-478.
[Andreev2] ^ A. Andreev, On convex polyhedra of finite volume in Lobacevskii spaces (in Russian), Math. Sbornik USSR, Nov. Ser. 83 (1970) 256-260.
Drawing Braids
(For In[1] see Setup)
| ||||
Thus for example,
In[3]:=
|
br = BR[5, {{1,3}, {-2,-4}, {1, 3}}];
|
In[4]:=
|
Show[BraidPlot[br]]
|
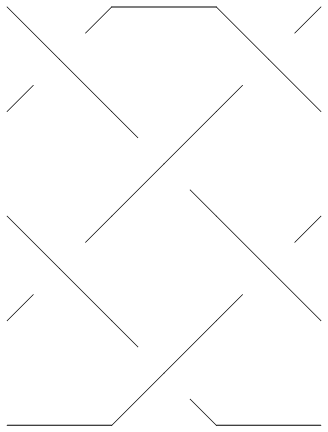
| |
Out[4]=
|
-Graphics-
|
BraidPlot takes several options:
In[5]:=
|
Options[BraidPlot]
|
Out[5]=
|
{Mode -> Graphics, Images -> {0.gif, 1.gif, 2.gif, 3.gif, 4.gif},
HTMLOpts -> , WikiOpts -> }
|
The Mode option to BraidPlot defaults to "Graphics", which produces output as above. An alternative is setting Mode -> "HTML", which produces an HTML <table> that can be readily inserted into HTML documents:
In[6]:=
|
BraidPlot[br, Mode -> "HTML"]
|
Out[6]=
|
<table cellspacing=0 cellpadding=0 border=0>
<tr><td><img src=1.gif><img src=0.gif><img src=1.gif></td></tr>
<tr><td><img src=2.gif><img src=3.gif><img src=2.gif></td></tr>
<tr><td><img src=1.gif><img src=4.gif><img src=1.gif></td></tr>
<tr><td><img src=2.gif><img src=3.gif><img src=2.gif></td></tr>
<tr><td><img src=0.gif><img src=4.gif><img src=0.gif></td></tr>
</table>
|
The table produced contains an array of image inclusions that together draws the braid using 5 fundamental building blocks: a horizontal "unbraided" line (0.gif above), the upper and lower halves of an overcrossing (1.gif and 2.gif above) and the upper and lower halves of an underfcrossing (3.gif and 4.gif above).
Assuming 0.gif through 4.gif are ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() , the above table is rendered as follows:
, the above table is rendered as follows:
The meaning of the Images option to BraidPlot should be clear from reading its default definition:
In[7]:=
|
Images /. Options[BraidPlot]
|
Out[7]=
|
{0.gif, 1.gif, 2.gif, 3.gif, 4.gif}
|
The HTMLOpts option to BraidPlot allows to insert options within the HTML <img> tags. Thus
In[8]:=
|
BraidPlot[BR[2, {1, 1}], Mode -> "HTML", HTMLOpts -> "border=1"]
|
Out[8]=
|
<table cellspacing=0 cellpadding=0 border=0>
<tr><td><img border=1 src=1.gif><img border=1 src=1.gif></td></tr>
<tr><td><img border=1 src=2.gif><img border=1 src=2.gif></td></tr>
</table>
|
The above table is rendered as follows:
| ||||
Thus compare the plots of br1 and br2 below:
In[10]:=
|
br1 = BR[TorusKnot[5, 4]]
|
Out[10]=
|
BR[4, {1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3}]
|
In[11]:=
|
Show[BraidPlot[br1]]
|
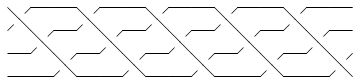
| |
Out[11]=
|
-Graphics-
|
In[12]:=
|
br2 = CollapseBraid[BR[TorusKnot[5, 4]]]
|
Out[12]=
|
BR[4, {{1}, {2}, {3, 1}, {2}, {3, 1}, {2}, {3, 1}, {2}, {3, 1}, {2},
{3}}]
|
In[13]:=
|
Show[BraidPlot[br2]]
|
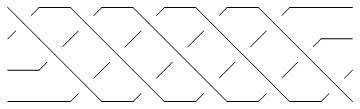
| |
Out[13]=
|
-Graphics-
|
Structure and Operations
(For In[1] see Setup)
| ||||
| ||||
| ||||
Thus here's one tautology and one easy example:
In[5]:=
|
Crossings /@ {Knot[0, 1], TorusKnot[11,10]}
|
Out[5]=
|
{0, 99}
|
And another easy example:
In[6]:=
|
K=Knot[6, 2]; {PositiveCrossings[K], NegativeCrossings[K]}
|
Out[6]=
|
{2, 4}
|
| ||||
| ||||
For example,
In[9]:=
|
PositiveQ /@ {X[1,3,2,4], X[1,4,2,3], Xp[1,3,2,4], Xp[1,4,2,3]}
|
Out[9]=
|
{False, True, True, True}
|
| ||||
The connected sum of the knot 4_1 with itself has 8 crossings (unsurprisingly):
In[11]:=
|
K = ConnectedSum[Knot[4,1], Knot[4,1]]
|
Out[11]=
|
ConnectedSum[Knot[4, 1], Knot[4, 1]]
|
In[12]:=
|
Crossings[K]
|
Out[12]=
|
8
|
It is also nice to know that, as expected, the Jones polynomial of is the square of the Jones polynomial of 4_1:
In[13]:=
|
Jones[K][q] == Expand[Jones[Knot[4,1]][q]^2]
|
Out[13]=
|
True
|
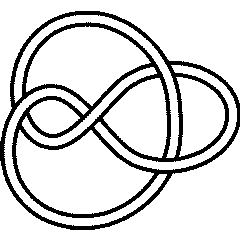 4_1 |
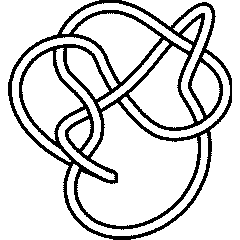 8_9 |
It is less nice to know that the Jones polynomial cannot tell apart from the knot 8_9:
In[14]:=
|
Jones[K][q] == Jones[Knot[8,9]][q]
|
Out[14]=
|
True
|
But isn't equivalent to 8_9; indeed, their Alexander polynomials are different:
In[15]:=
|
{Alexander[K][t], Alexander[Knot[8,9]][t]}
|
Out[15]=
|
-2 6 2 -3 3 5 2 3
{11 + t - - - 6 t + t , 7 - t + -- - - - 5 t + 3 t - t }
t 2 t
t
|
Invariants
- Invariants from Braid Theory
- Three Dimensional Invariants
- The Alexander-Conway Polynomial
- The Multivariable Alexander Polynomial
- The Determinant and the Signature
- The Jones Polynomial
- The Coloured Jones Polynomials
- The A2 Invariant
- Quantum knot invariants
- The HOMFLY-PT Polynomial
- The Kauffman Polynomial
- Finite Type (Vassiliev) Invariants
- Khovanov Homology
- Heegaard Floer Knot Homology
- R-Matrix Invariants
Invariants from Braid Theory
The braid length of a knot or a link is the smallest number of crossings in a braid whose closure is . KnotTheory` has some braid lengths preloaded:
(For In[1] see Setup)
| ||||
Note that the braid length of is simply the length of the minimum braid representing (see Braid Representatives):
In[3]:=
|
K = Knot[9, 49]; {BraidLength[K], Crossings[BR[K]]}
|
Out[3]=
|
{11, 11}
|
 9_49 |
 10_136 |
The braid index of a knot or a link is the smallest number of strands in a braid whose closure is . KnotTheory` has some braid indices preloaded:
|
| ||||||||
Of the 250 knots with up to 10 crossings, only 10_136 has braid index smaller than the width of its minimum braid:
In[6]:=
|
K = Knot[10, 136]; {BraidIndex[K], First@BR[K]}
|
Out[6]=
|
{4, 5}
|
In[7]:=
|
Show[BraidPlot[BR[K]]]
|
| |
Out[7]=
|
-Graphics-
|
Three Dimensional Invariants
(For In[1] see Setup)
Symmetry Type
|
| ||||||||
The inverse of a knot is the knot obtained from it by reversing its parametrization. The mirror of A knot is obtained from by reversing the orientation of the ambient space, or, alternatively, by flipping all the crossings of .
A knot is called "fully amphicheiral" if it is equal to its inverse and also to its mirror. The first knot with this property is
In[4]:=
|
Select[AllKnots[],
(SymmetryType[#] == FullyAmphicheiral) &, 1]
|
Out[4]=
|
{Knot[4, 1]}
|
A knot is called "reversible" if it is equal to its inverse yet it different from its mirror (and hence also from the inverse of its mirror). Many knots have this property; indeed, the first one is:
In[5]:=
|
Select[AllKnots[],
(SymmetryType[#] == Reversible) &, 1]
|
Out[5]=
|
{Knot[3, 1]}
|
A knot is called "positive amphicheiral" if it is different from its inverse but equal to its mirror. There are no such knots with up to 11 crossings.
A knot is called "negative amphicheiral" if it is different from its inverse and its mirror, yet it is equal to the inverse of its mirror. The first knot with this property is
In[6]:=
|
Select[AllKnots[],
(SymmetryType[#] == NegativeAmphicheiral) &, 1]
|
Out[6]=
|
{Knot[8, 17]}
|
Finally, if a knot is different from its inverse, its mirror and from the inverse of its mirror, it is "chiral". The first such knot is
In[7]:=
|
Select[AllKnots[],
(SymmetryType[#] == Chiral) &, 1]
|
Out[7]=
|
{Knot[9, 32]}
|
It is a amusing to take "symmetry type" statistics on all the prime knots with up to 11 crossings:
In[8]:=
|
Plus @@ (SymmetryType /@ Rest[AllKnots[]])
|
Out[8]=
|
216 Chiral + 13 FullyAmphicheiral + 7 NegativeAmphicheiral +
565 Reversible
|
 4_1 |
 3_1 |
 8_17 |
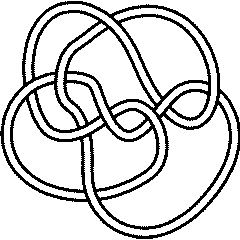 9_32 |
Unknotting Number
The unknotting number of a knot is the minimal number of crossing changes needed in order to unknot .
|
| ||||||||
Of the 512 knots whose unknotting number is known to KnotTheory`, 197 have unknotting number 1, 247 have unknotting number 2, 54 have unknotting number 3, 12 have unknotting number 4 and 1 has unknotting number 5:
In[11]:=
|
Plus @@ u /@ Cases[UnknottingNumber /@ AllKnots[], _Integer]
|
Out[11]=
|
u[0] + 197 u[1] + 247 u[2] + 54 u[3] + 12 u[4] + u[5]
|
There are 4 knots with up to 9 crossings whose unknotting number is unknown:
In[12]:=
|
Select[AllKnots[],
Crossings[#] <= 9 && Head[UnknottingNumber[#]] === List &
]
|
Out[12]=
|
{Knot[9, 10], Knot[9, 13], Knot[9, 35], Knot[9, 38]}
|
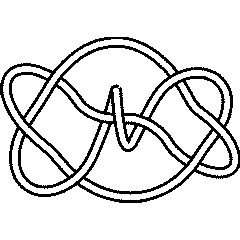 9_10 |
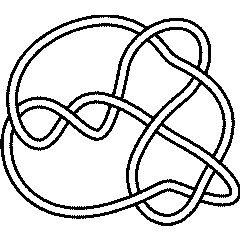 9_13 |
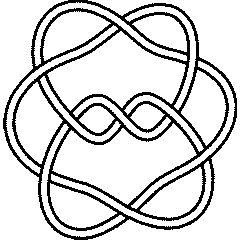 9_35 |
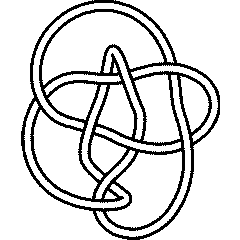 9_38 |
3-Genus
A Seifert surface for a knot is a compact oriented surface with boundary . Seifert surfaces exist, but are not unique. The SeifertView programme is a visual implementation of the algorithm of Seifert (1934) for the construction of a Seifert surface from a knot projection. The 3-genus of a knot is the minimal genus of a Seifert surface for that knot.
|
| ||||||||
The highest 3-genus of the knots known to KnotTheory` is , and there is only one knot with up to 11 crossings whose 3-genus is 5:
In[15]:=
|
Max[ThreeGenus /@ AllKnots[]]
|
Out[15]=
|
5
|
In[16]:=
|
Select[AllKnots[], ThreeGenus[#] == 5 &]
|
Out[16]=
|
{Knot[11, Alternating, 367]}
|
 K11a367 |
 T(11,2) |
(K11a367 is, of couse, also known as the torus knot T(11,2)).
The Conway knot K11n34 is the closure of the braid BR[4, {1, 1, 2, -3, 2, 1, -3, -2, -2, -3, -3}]. Let us compute its 3-genus and compare it with the 3-genus of its mutant companion, the Kinoshita-Terasaka knot K11n42:
In[17]:=
|
ThreeGenus[BR[4, {1, 1, 2, -3, 2, 1, -3, -2, -2, -3, -3}]]
|
Out[17]=
|
3
|
In[18]:=
|
ThreeGenus[Knot[11, NonAlternating, 42]]
|
Out[18]=
|
2
|
 K11n34 |
 K11n42 |
Bridge Index
The bridge index' of a knot is the minimal number of local maxima (or local minima) in a generic smooth embedding of in .
|
| ||||||||
An often studied class of knots is the class of 2-bridge knots, knots whose bridge index is 2. Of the 49 prime 9-crossings knots, 24 are 2-bridge:
In[21]:=
|
Select[AllKnots[], Crossings[#] == 9 && BridgeIndex[#] == 2 &]
|
Out[21]=
|
{Knot[9, 1], Knot[9, 2], Knot[9, 3], Knot[9, 4], Knot[9, 5],
Knot[9, 6], Knot[9, 7], Knot[9, 8], Knot[9, 9], Knot[9, 10],
Knot[9, 11], Knot[9, 12], Knot[9, 13], Knot[9, 14], Knot[9, 15],
Knot[9, 17], Knot[9, 18], Knot[9, 19], Knot[9, 20], Knot[9, 21],
Knot[9, 23], Knot[9, 26], Knot[9, 27], Knot[9, 31]}
|
Super Bridge Index
The super bridge index of a knot is the minimal number, in a generic smooth embedding of in , of the maximal number of local maxima (or local minima) in a rigid rotation of that projection.
|
| ||||||||
Nakanishi Index
|
| ||||||||
Synthesis
In[26]:=
|
Profile[K_] := Profile[
SymmetryType[K], UnknottingNumber[K], ThreeGenus[K],
BridgeIndex[K], SuperBridgeIndex[K], NakanishiIndex[K]
]
|
In[27]:=
|
Profile[Knot[9,24]]
|
Out[27]=
|
Profile[Reversible, 1, 3, 3, {4, 6}, 1]
|
In[28]:=
|
Ks = Select[AllKnots[], (Crossings[#] == 9 && Profile[#]==Profile[Knot[9,24]])&]
|
Out[28]=
|
{Knot[9, 24], Knot[9, 28], Knot[9, 30], Knot[9, 34]}
|
 9_24 |
 9_28 |
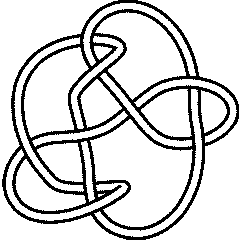 9_30 |
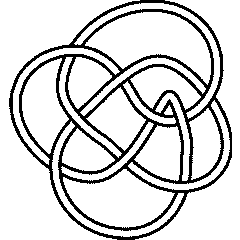 9_34 |
In[29]:=
|
Alexander[#][t]& /@ Ks
|
Out[29]=
|
-3 5 10 2 3
{13 - t + -- - -- - 10 t + 5 t - t ,
2 t
t
-3 5 12 2 3
-15 + t - -- + -- + 12 t - 5 t + t ,
2 t
t
-3 5 12 2 3
17 - t + -- - -- - 12 t + 5 t - t ,
2 t
t
-3 6 16 2 3
23 - t + -- - -- - 16 t + 6 t - t }
2 t
t
|
The Alexander-Conway Polynomial
(For In[1] see Setup)
|
| ||||||||
| ||||
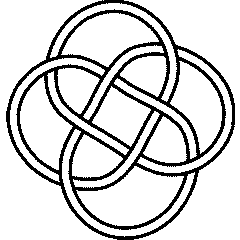 8_18 |
The Alexander polynomial and the Conway polynomial of a knot always satisfy . Let us verify this relation for the knot 8_18:
In[5]:=
|
alex = Alexander[Knot[8, 18]][t]
|
Out[5]=
|
-3 5 10 2 3
13 - t + -- - -- - 10 t + 5 t - t
2 t
t
|
In[6]:=
|
Expand[Conway[Knot[8, 18]][Sqrt[t] - 1/Sqrt[t]]]
|
Out[6]=
|
-3 5 10 2 3
13 - t + -- - -- - 10 t + 5 t - t
2 t
t
|
The determinant of a knot is . Hence for 8_18 it is
In[7]:=
|
Abs[alex /. t -> -1]
|
Out[7]=
|
45
|
Alternatively (see The Determinant and the Signature):
In[8]:=
|
KnotDet[Knot[8, 18]]
|
Out[8]=
|
45
|
, the (standardly normalized) type 2 Vassiliev invariant of a knot is the coefficient of in its Conway polynomial:
In[9]:=
|
Coefficient[Conway[Knot[8, 18]][z], z^2]
|
Out[9]=
|
1
|
Alternatively (see Finite Type (Vassiliev) Invariants),
In[10]:=
|
Vassiliev[2][Knot[8, 18]]
|
Out[10]=
|
1
|
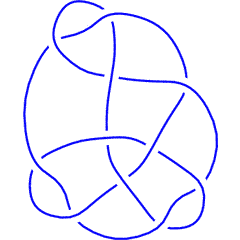 K11a99 |
 K11a277 |
Sometimes two knots have the same Alexander polynomial but different Alexander ideals. An example is the pair K11a99 and K11a277. They have the same Alexander polynomial, but the second Alexander ideal of the first knot is the whole ring while the second Alexander ideal of the second knot is the smaller ideal generated by and by :
In[11]:=
|
{K1, K2} = {Knot[11, Alternating, 99], Knot[11, Alternating, 277]};
|
In[12]:=
|
Alexander[K1] == Alexander[K2]
|
Out[12]=
|
True
|
In[13]:=
|
Alexander[K1, 2][t]
|
Out[13]=
|
{1}
|
In[14]:=
|
Alexander[K2, 2][t]
|
Out[14]=
|
{3, 1 + t}
|
Finally, the Alexander polynomial attains 551 values on the 802 knots known to KnotTheory`:
In[15]:=
|
Length /@ {Union[Alexander[#]& /@ AllKnots[]], AllKnots[]}
|
Out[15]=
|
{551, 802}
|
The Determinant and the Signature
(For In[1] see Setup)
| ||||
| ||||
Thus, for example, the knots 5_1 and 10_132 have the same determinant (and even the same Alexander and Jones polynomials), but different signatures:
 5_1 |
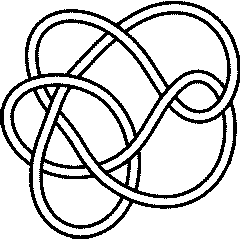 10_132 |
In[4]:=
|
KnotDet /@ {Knot[5, 1], Knot[10, 132]}
|
Out[4]=
|
{5, 5}
|
In[5]:=
|
{
Equal @@ (Jones[#][q]& /@ {Knot[5, 1], Knot[10, 132]}),
Equal @@ (Alexander[#][t]& /@ {Knot[5, 1], Knot[10, 132]})
}
|
Out[5]=
|
{True, True}
|
In[6]:=
|
KnotSignature /@ {Knot[5, 1], Knot[10, 132]}
|
Out[6]=
|
{-4, 0}
|
In August 2005 somebody emailed Dror a question about knot colouring, which amounted to "find the first knot (other than the unknot) whose determinant is ". So on September 2nd Dror typed
In[7]:=
|
Select[AllKnots[], Abs[KnotDet[#]] == 1 &]
|
Out[7]=
|
{Knot[0, 1], Knot[10, 124], Knot[10, 153],
Knot[11, NonAlternating, 34], Knot[11, NonAlternating, 42],
Knot[11, NonAlternating, 49], Knot[11, NonAlternating, 116]}
|
Hence the first few knots that are not -colourable for any are 10_124, 10_153, K11n34, K11n42, K11n49 and K11n116.
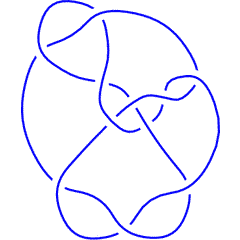 K11n116 |
The Jones Polynomial
(For In[1] see Setup)
| ||||
In Naming and Enumeration we checked that the knots 6_1 and 9_46 have the same Alexander polynomial. Their Jones polynomials are different, though:
In[3]:=
|
Jones[Knot[6, 1]][q]
|
Out[3]=
|
-4 -3 -2 2 2
2 + q - q + q - - - q + q
q
|
In[4]:=
|
Jones[Knot[9, 46]][q]
|
Out[4]=
|
-6 -5 -4 2 -2 1
2 + q - q + q - -- + q - -
3 q
q
|
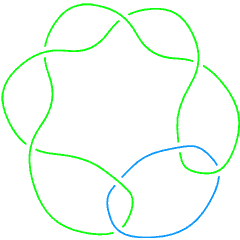 L8a6 |
On links with an even number of components the Jones polynomial is a function of , and hence it is often more convenient to view it as a function of , where :
In[5]:=
|
Jones[Link[8, Alternating, 6]][q]
|
Out[5]=
|
-(9/2) -(7/2) 3 3 4 3/2
-q + q - ---- + ---- - ------- + 3 Sqrt[q] - 2 q +
5/2 3/2 Sqrt[q]
q q
5/2 7/2
2 q - q
|
In[6]:=
|
PowerExpand[Jones[Link[8, Alternating, 6]][t^2]]
|
Out[6]=
|
-9 -7 3 3 4 3 5 7
-t + t - -- + -- - - + 3 t - 2 t + 2 t - t
5 3 t
t t
|
The Jones polynomial attains 2110 values on the 2226 knots and links known to KnotTheory`:
In[7]:=
|
all = Join[AllKnots[], AllLinks[]];
|
In[8]:=
|
Length /@ {Union[Jones[#][q]& /@ all], all}
|
Out[8]=
|
{2110, 2226}
|
How is the Jones polynomial computed?
(See also: The Kauffman Bracket using Haskell)
The Jones polynomial is so simple to compute using Mathematica that it's worthwhile pause and see how this is done, even for readers with limited prior programming experience. First, recall (say from [Kauffman]) the definition of the Jones polynomial using the Kauffman bracket :
| [KBDef] |
here is a commutative variable, , and is the writhe of , the difference where and count the positive Failed to parse (unknown function "\overcrossing"): {\displaystyle (\overcrossing)} and negative Failed to parse (unknown function "\undercrossing"): {\displaystyle (\undercrossing)} crossings of respectively.
Just for concreteness, let us start by fixing to be the trefoil knot shown above:
In[9]:=
|
L = PD[Knot[3, 1]]
|
Out[9]=
|
PD[X[1, 4, 2, 5], X[3, 6, 4, 1], X[5, 2, 6, 3]]
|
Our first task is to perform the replacement Failed to parse (unknown function "\slashoverback"): {\displaystyle \langle\slashoverback\rangle\to A\langle\hsmoothing\rangle + B\langle\smoothing\rangle} on all crossings of . By our conventions (see Planar Diagrams) the edges around a crossing are labeled , , and : Failed to parse (unknown function "\slashoverback"): {\displaystyle {}^c_d\slashoverback{}_a^b} . Labeling the smoothings Failed to parse (unknown function "\hsmoothing"): {\displaystyle (\hsmoothing, \ \smoothing)} in the same way, Failed to parse (unknown function "\hsmoothing"): {\displaystyle {}^c_d\hsmoothing{}_a^b} and Failed to parse (unknown function "\smoothing"): {\displaystyle {}^c_d\smoothing{}_a^b} , we are lead to the symbolic replacement rule . Let us apply this rule to , switch to a multiplicative notation and expand:
In[10]:=
|
t1 = L /. X[a_,b_,c_,d_] :> A P[a,d] P[b,c] + B P[a,b] P[c,d]
|
Out[10]=
|
PD[A P[1, 5] P[2, 4] + B P[1, 4] P[2, 5],
B P[1, 4] P[3, 6] + A P[1, 3] P[4, 6],
A P[2, 6] P[3, 5] + B P[2, 5] P[3, 6]]
|
In[11]:=
|
t2 = Expand[Times @@ t1]
|
Out[11]=
|
2
A B P[1, 4] P[1, 5] P[2, 4] P[2, 6] P[3, 5] P[3, 6] +
2 2
A B P[1, 4] P[2, 5] P[2, 6] P[3, 5] P[3, 6] +
2 2
A B P[1, 4] P[1, 5] P[2, 4] P[2, 5] P[3, 6] +
3 2 2 2
B P[1, 4] P[2, 5] P[3, 6] +
3
A P[1, 3] P[1, 5] P[2, 4] P[2, 6] P[3, 5] P[4, 6] +
2
A B P[1, 3] P[1, 4] P[2, 5] P[2, 6] P[3, 5] P[4, 6] +
2
A B P[1, 3] P[1, 5] P[2, 4] P[2, 5] P[3, 6] P[4, 6] +
2 2
A B P[1, 3] P[1, 4] P[2, 5] P[3, 6] P[4, 6]
|
In the above expression the product P[1,4] P[1,5] P[2,4] P[2,6] P[3,5] P[3,6] represents a path in which 1 is connected to 4, 1 is connected to 5, 2 is connected to 4, etc. (see the right half of the figure above). We simplify such paths by repeatedly applying the rules and :
In[12]:=
|
t3 = t2 //. {P[a_,b_]P[b_,c_] :> P[a,c], P[a_,b_]^2 :> P[a,a]}
|
Out[12]=
|
3 2
B P[1, 1] P[2, 2] P[3, 3] + A B P[2, 2] P[4, 4] +
3 2 2
A P[3, 3] P[4, 4] + A B P[3, 3] P[4, 4] + 3 A B P[5, 5] +
2
A B P[1, 1] P[5, 5]
|
To complete the computation of the Kauffman bracket, all that remains is to replace closed cycles (paths of the form by , to replace by , and to simplify:
In[13]:=
|
t4 = Expand[t3 /. P[a_,a_] -> -A^2-B^2 /. B -> 1/A]
|
Out[13]=
|
-9 1 3 7
-A + - + A + A
A
|
We could have, of course, combined the above four lines to a single very short program, that compues the Kauffman bracket from the beginning to the end:
In[14]:=
|
KB0[pd_] := Expand[
Expand[Times @@ pd /. X[a_,b_,c_,d_] :> A P[a,d] P[b,c] + 1/A P[a,b] P[c,d]]
//. {P[a_,b_]P[b_,c_] :> P[a,c], P[a_,b_]^2 :> P[a,a], P[a_,a_] -> -A^2-1/A^2}]
|
In[15]:=
|
t4 = KB0[PD[Knot[3, 1]]]
|
Out[15]=
|
-9 1 3 7
-A + - + A + A
A
|
We will skip the uninteresting code for the computation of the writhe here; it is a linear time computation, and if that's all we ever wanted to compute, we wouldn't have bothered to purchase a computer. For our the result is , and hence the Jones polynomial of is given by
In[16]:=
|
(-A^3)^(-3) * t4 / (-A^2-1/A^2) /. A -> q^(1/4) // Simplify // Expand
|
Out[16]=
|
-4 -3 1
-q + q + -
q
|
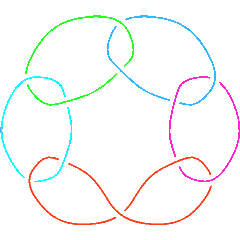 L11a548 |
At merely 3 lines of code, our program is surely nice and elegant. But it is very slow:
In[17]:=
|
time0 = Timing[KB0[PD[Link[11, Alternating, 548]]]]
|
Out[17]=
|
-23 5 10 -3 5 13 17 21 25
{1., A + --- + -- + A + 6 A + 6 A + 5 A - 5 A + 4 A - A }
15 7
A A
|
Here's the much faster alternative employed by KnotTheory`:
In[18]:=
|
KB1[pd_PD] := KB1[pd, {}, 1];
KB1[pd_PD, inside_, web_] := Module[
{pos = First[Ordering[Length[Complement[List @@ #, inside]]& /@ pd]]},
pd[[pos]] /. X[a_,b_,c_,d_] :> KB1[
Delete[pd, pos],
Union[inside, {a,b,c,d}],
Expand[web*(A P[a,d] P[b,c]+1/A P[a,b] P[c,d])] //. {
P[e_,f_]P[f_,g_] :> P[e,g], P[e_,_]^2 :> P[e,e], P[e_,e_] -> -A^2-1/A^2
}
]
];
KB1[PD[],_,web_] := Expand[web]
|
In[19]:=
|
time1 = Timing[KB1[PD[Link[11, Alternating, 548]]]]
|
Out[19]=
|
-23 5 10 -3 5 13 17 21
{0.015, A + --- + -- + A + 6 A + 6 A + 5 A - 5 A + 4 A -
15 7
A A
25
A }
|
(So on L11a548 KB1 is -23 5 10 -3 5 13 17 21 25
{1., A + --- + -- + A + 6 A + 6 A + 5 A - 5 A + 4 A - A }1,1
15 7
A A/ -23 5 10 -3 5 13 17 21 25
{0.015, A + --- + -- + A + 6 A + 6 A + 5 A - 5 A + 4 A - A }1,1
15 7
A A ~ -23 5 10 -3 5 13 17 21 25
{1., A + --- + -- + A + 6 A + 6 A + 5 A - 5 A + 4 A - A }1,1
15 7
A A
Round[--------------------------------------------------------------------------------]
-23 5 10 -3 5 13 17 21 25
{0.015, A + --- + -- + A + 6 A + 6 A + 5 A - 5 A + 4 A - A }1,1
15 7
A A times faster than KB0.)
The idea here is to maintain a "computation front", a planar domain which starts empty and gradualy increases until the whole link diagram is enclosed. Within the front, the rules defining the Kauffman bracket, Equation [KBDef], are applied and the result is expanded as much as possible. Outside of the front the link diagram remains untouched. At every step we choose a crossing outside the front with the most legs inside and "conquer" it -- apply the rules of [KBDef] and expand again. As our new outpost is maximally connected to our old territory, the length of the boundary is increased in a minimal way, and hence the size of the "web" within our front remains as small as possible and thus quick to manipulate.
In further detail, the routine KB1[pd, inside, web] computes the
Kauffman bracket assuming the labels of the edges inside the front are in
the variable inside, the already-computed inside of the front is in
the variable web and the part of the link diagram yet untouched is
pd. The single argument KB1[pd] simply calls
KB1[pd, inside, web] with an empty inside and with web set to 1. The three argument KB1[pd, inside, web] finds the position of the crossing maximmally connected to the front using the somewhat
cryptic assignment
pos = First[Ordering[Length[Complement[List @@ #, inside]]& /@ pd]]}
KB1[pd, inside, web] then recursively calls
itself with that crossing removed from pd}, with its legs
added to the inside, and with web updated in accordance
with [KBDef]. Finally, when pd is empty, the output is
simply the value of web.
[Kauffman] ^ L. H. Kauffman, On knots, Princeton Univ. Press, Princeton, 1987.
The Coloured Jones Polynomials
KnotTheory` can compute the coloured Jones polynomial of knots and links, using the formulas in [Garoufalidis Le]:
(For In[1] see Setup)
In[2]:=
?ColouredJones
ColouredJones[K, n][q] returns the coloured Jones polynomial of a knot in colour n (i.e., in the (n+1)-dimensional representation) in the indeterminate q. Some of these polynomials have been precomputed in KnotTheory`. To force computation, use ColouredJones[K,n, Program -> "prog"][q], with "prog" replaced by one of the two available programs, "REngine" or "Braid" (including the quotes). "REngine" (default) computes the invariant for closed knots (as well as links where all components are coloured by the same integer) directly from the MorseLink presentation of the knot, while "Braid" computes the invariant via a presentation of the knot as a braid closure. "REngine" will usually be faster, but it might be better to use "Braid" when (roughly): 1) a "good" braid representative is available for the knot, and 2) the length of this braid is less than the maximum width of the MorseLink presentation of the knot.
In[3]:=
ColouredJones::about
The "REngine" algorithm was written by Siddarth Sankaran in the summer of 2005, while the "Braid" algorithm was written jointly by Dror Bar-Natan and Stavros Garoufalidis. Both are based on formulas by Thang Le and Stavros Garoufalidis; see [Garoufalidis, S. and Le, T. "The coloured Jones function is q-holonomic." Geom. Top., v9, 2005 (1253-1293)].
Thus, for example, here's the coloured Jones polynomial of the knot
4_1 in the 4-dimensional representation of :
In[4]:=
ColouredJones[Knot[4, 1], 3][q]
Out[4]=
-12 -11 -10 2 2 3 3 2 4 6
3 + q - q - q + -- - -- + -- - -- - 3 q + 3 q - 2 q +
8 6 4 2
q q q q
8 10 11 12
2 q - q - q + q
And here's the coloured Jones polynomial of the same knot in the two
dimensional representation of ; this better be equal to the ordinary
Jones polynomial of 4_1!
In[5]:=
ColouredJones[Knot[4, 1], 1][q]
Out[5]=
-2 1 2
1 + q - - - q + q
q
In[6]:=
Jones[Knot[4, 1]][q]
Out[6]=
-2 1 2
1 + q - - - q + q
q
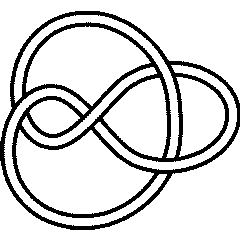
4_1
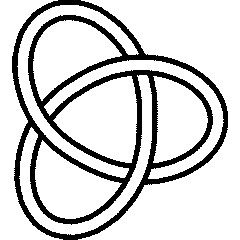
3_1
In[7]:=
?CJ`Summand
CJ`Summand[br, n] returned a pair {s, vars} where s is the summand in the the big sum that makes up ColouredJones[br, n][q] and where vars is the list of variables that need to be summed over (from 0 to n) to get ColouredJones[br, n][q]. CJ`Summand[K, n] is the same for knots for which a braid representative is known to this program.
The coloured Jones polynomial of 3_1 is computed via a single summation. Indeed,
In[8]:=
s = CJ`Summand[Mirror[Knot[3, 1]], n]
Out[8]=
(3 n)/2 + n CJ`k[1] + (-n + 2 CJ`k[1])/2 1
{CJ`q qBinomial[0, 0, ----]
CJ`q
1 1
qBinomial[CJ`k[1], 0, ----] qBinomial[CJ`k[1], CJ`k[1], ----]
CJ`q CJ`q
n 1 n 1
qPochhammer[CJ`q , ----, 0] qPochhammer[CJ`q , ----, CJ`k[1]]
CJ`q CJ`q
n - CJ`k[1] 1
qPochhammer[CJ`q , ----, 0], {CJ`k[1]}}
CJ`q
The symbols in the above formula require a definition:
In[9]:=
?qPochhammer
qPochhammer[a, q, k] represents the q-shifted factorial of a in base q with index k. See Eric Weisstein's
http://mathworld.wolfram.com/q-PochhammerSymbol.html and Axel Riese's
www.risc.uni-linz.ac.at/research/combinat/risc/software/qMultiSum/
In[10]:=
?qBinomial
qBinomial[n, k, q] represents the q-binomial coefficient of n and k in base q. For k<0 it is 0; otherwise it is
qPochhammer[q^(n-k+1), q, k] / qPochhammer[q, q, k].
More precisely, qPochhammer[a, q, k] is
and qBinomial[n, k, q] is
The function qExpand replaces every occurence of a qPochhammer[a, q, k]
symbol or a qBinomial[n, k, q] symbol by its definition:
In[11]:=
?qExpand
qExpand[expr_] replaces all occurences of qPochhammer and qBinomial in expr by their definitions as products. See the documentation for qPochhammer and for qBinomial for details.
Hence,
In[12]:=
qPochhammer[a, q, 6] // qExpand
Out[12]=
2 3 4 5
(-1 + a) (-1 + a q) (-1 + a q ) (-1 + a q ) (-1 + a q ) (-1 + a q )
In[13]:=
First[s] /. {n -> 3, CJ`k[1] -> 2} // qExpand
Out[13]=
11 2 3
CJ`q (-1 + CJ`q ) (-1 + CJ`q )
Finally,
In[14]:=
?ColoredJones
Type ColoredJones and see for yourself.
[Garoufalidis Le] ^ S. Garoufalidis and T. Q. T. Le, The Colored Jones Function is -Holonomic, Georgia Institute of Technology preprint, September 2003, arXiv:math.GT/0309214.
The A2 Invariant
We compute the (or quantum ) invariant using the normalization and formulas of [Khovanov], which in itself follows [Kuperberg]:
(For In[1] see Setup)
In[2]:=
?A2Invariant
A2Invariant[L][q] computes the A2 (sl(3)) invariant of a knot or link L as a function of the variable q.
As an example, let us check that the knots 10_22 and 10_35 have the same Jones polynomial but different invariants:
In[3]:=
Jones[Knot[10, 22]][q] == Jones[Knot[10, 35]][q]
Out[3]=
True
In[4]:=
A2Invariant[Knot[10, 22]][q]
Out[4]=
-12 -8 -6 -4 2 4 6 8 10 12 14
-1 + q + q + q - q + -- - q - 2 q + q - q + q + q +
2
q
18
q
In[5]:=
A2Invariant[Knot[10, 35]][q]
Out[5]=
-14 -12 -10 -8 2 2 2 6 8 10 14 16
q + q - q + q - -- + -- + q - q + q - 2 q + q - q +
4 2
q q
18 20
q + q
The invariant attains 2163 values on the 2226 knots and links known to KnotTheory:
In[6]:=
all = Join[AllKnots[], AllLinks[]];
In[7]:=
Length /@ {Union[A2Invariant[#][q]& /@ all], all}
Out[7]=
{2163, 2226}
[Khovanov] ^ M. Khovanov, link homology I, arXiv:math.QA/0304375.
[Kuperberg] ^ G. Kuperberg, Spiders for rank 2 Lie algebras, Comm. Math. Phys. 180 (1996) 109-151, arXiv:q-alg/9712003.
The HOMFLY-PT Polynomial
The HOMFLY-PT polynomial (see [HOMFLY] and [PT]) of a knot or link is defined by the skein relation
Failed to parse (unknown function "\overcrossing"): {\displaystyle aH\left(\overcrossing\right)-a^{-1}H\left(\undercrossing\right)=zH\left(\smoothing\right) }
and by the initial condition =1.
KnotTheory` knows about the HOMFLY-PT polynomial:
(For In[1] see Setup)
In[2]:=
?HOMFLYPT
HOMFLYPT[K][a, z] computes the HOMFLY-PT (Hoste, Ocneanu, Millett, Freyd, Lickorish, Yetter, Przytycki and Traczyk) polynomial of a knot/link K, in the variables a and z.
In[3]:=
HOMFLYPT::about
The HOMFLYPT program was written by Scott Morrison.
Thus, for example, here's the HOMFLY-PT polynomial of the knot 8_1:
In[4]:=
K = Knot[8, 1];
In[5]:=
HOMFLYPT[Knot[8, 1]][a, z]
Out[5]=
-2 4 6 2 2 2 4 2
a - a + a - z - a z - a z
It is well known that HOMFLY-PT polynomial specializes to the Jones polynomial at and and to the Conway polynomial at . Indeed,
In[6]:=
Expand[HOMFLYPT[K][1/q, Sqrt[q]-1/Sqrt[q]]]
Out[6]=
-6 -5 -4 2 2 2 2
2 + q - q + q - -- + -- - - - q + q
3 2 q
q q
In[7]:=
Jones[K][q]
Out[7]=
-6 -5 -4 2 2 2 2
2 + q - q + q - -- + -- - - - q + q
3 2 q
q q
In[8]:=
{HOMFLYPT[K][1, z], Conway[K][z]}
Out[8]=
2 2
{1 - 3 z , 1 - 3 z }
8_1
L5a1
In our parametrization of the link invariant, it satisfies
, where is some knot or link and where is the number of components of . Let us verify this fact for the Whitehead link, L5a1:
In[9]:=
L = Link[5, Alternating, 1];
In[10]:=
Simplify[{
(-1)^(Length[Skeleton[L]]-1)(q^2+1+1/q^2)HOMFLYPT[L][1/q^3, q-1/q],
A2Invariant[L][q]
}]
Out[10]=
-12 -8 -6 2 -2 2 4 6
{2 - q + q + q + -- + q + q + q + q ,
4
q
-12 -8 -6 2 -2 2 4 6
2 - q + q + q + -- + q + q + q + q }
4
q
Other Software to Compute the HOMFLY-PT Polynomial
A C-based program running under windows by M. Ochiai can compute the HOMFLY-PT polynomial of certain knots and links with up to hundreds of crossings using "base tangle decompositions". His program, bTd, is available at [1].
References
[HOMFLY] ^ J. Hoste, A. Ocneanu, K. Millett, P. Freyd, W. B. R. Lickorish and D. Yetter, A new polynomial invariant of knots and links, Bull. Amer. Math. Soc. 12 (1985) 239-246.
[PT] ^ J. Przytycki and P. Traczyk, Conway Algebras and Skein Equivalence of Links, Proc. Amer. Math. Soc. 100 (1987) 744-748.
The Kauffman Polynomial
The Kauffman polynomial (see [Kauffman]) of a knot or link is where is the writhe of (see How is the Jones Polynomial Computed?) and where is the regular isotopy invariant defined by the skein relations
(here is a strand and is the same strand with a kink added) and
Failed to parse (unknown function "\backoverslash"): {\displaystyle L(\backoverslash)+L(\slashoverback) = z\left(L(\smoothing)+L(\hsmoothing)\right)}
and by the initial condition where is the unknot  .
.
KnotTheory` knows about the Kauffman polynomial:
(For In[1] see Setup)
In[2]:=
?Kauffman
Kauffman[K][a, z] computes the Kauffman polynomial of a knot or link K, in the variables a and z.
In[3]:=
Kauffman::about
The Kauffman polynomial program was written by Scott Morrison.
Thus, for example, here's the Kauffman polynomial of the knot 5_2:
In[4]:=
Kauffman[Knot[5, 2]][a, z]
Out[4]=
2 4 6 5 7 2 2 4 2 6 2 3 3
-a + a + a - 2 a z - 2 a z + a z - a z - 2 a z + a z +
5 3 7 3 4 4 6 4
2 a z + a z + a z + a z

5_2

T(8,3)
It is well known that the Jones polynomial is related to the Kauffman polynomial via
, where is some knot or link and where is the number of components of . Let us verify this fact for the torus knot T(8,3):
In[5]:=
K = TorusKnot[8, 3];
In[6]:=
Simplify[{
(-1)^(Length[Skeleton[K]]-1)Kauffman[K][-q^(-3/4), q^(1/4)+q^(-1/4)],
Jones[K][q]
}]
Out[6]=
7 9 16 7 9 16
{q + q - q , q + q - q }
[Kauffman] ^ L. H. Kauffman, An invariant of regular isotopy, Trans. Amer. Math. Soc. 312 (1990) 417-471.
Finite Type (Vassiliev) Invariants
(For In[1] see Setup)
In[2]:=
?Vassiliev
Vassiliev[2][K] computes the (standardly normalized) type 2 Vassiliev invariant of the knot K, i.e., the coefficient of z^2 in Conway[K][z]. Vassiliev[3][K] computes the (standardly normalized) type 3 Vassiliev invariant of the knot K, i.e., 3J''(1)-(1/36)J'''(1) where J is the Jones polynomial of K.
Thus, for example, let us reproduce Willerton's "fish" (arXiv:math.GT/0104061), the result of plotting the values of against the values of , where is the (standardly normalized) type 2 invariant of , is the (standardly normalized) type 3 invariant of , and where runs over a set of knots with equal crossing numbers (10, in the example below):
As another example, let us consider the expansion of the Jones polynomial for a knot as a power series in when we substitute the standard variable with and use the power series expansion of :
Then, for the above coefficients we have that and for all is a Vassiliev invariant of type [BirmanLin].
We can see this result by using the invariant formula:
Failed to parse (unknown function "\doublepoint"): {\displaystyle V\left(\doublepoint\right)= V\left(\overcrossing\right)-V\left(\undercrossing\right)}
to check the Birman-Lin condition, which tells us that an invariant is of type if it vanishes on knots with more than double points, or self intersections (see [Bar-Natan]). Computing on knots with more than one double point by resolving one self intersection at a time, it is enough to check that vanishes on knots with double points:
Failed to parse (unknown function "\doublepoint"): {\displaystyle V\underbrace{ \left(\doublepoint\cdots\doublepoint\right) }_{m+1}=0}
The following two programs let us determine for any integer and knot :
In[4]:=
SetCrossing[K_, l_Integer, s_] := Module[
{pd, n},
pd = PD[K];
If[PositiveQ[pd[[l]]],
If[s == "-", pd[[l]] = RotateRight@pd[[l]]],
If[s == "+", pd[[l]] = RotateLeft@pd[[l]]]];
pd];
In[5]:=
V[K_, n_] := Series[Jones[K][Exp[x]], {x, 0, n}];
V[K_, n_, {i1_, is___}] :=
V[SetCrossing[K, i1, "+"], n, {is}] -
V[SetCrossing[K, i1, "-"], n, {is}];
V[K_, n_, {}] := V[K, n];
The first program, SetCrossing, sets the crossing of a knot to be positive or negative depending on whether we choose to be "" or "". The second program uses the invariant formula to give the series expansion of the Jones polynomial of a knot discussed above, up to order , where a selected list of the crossings of are taken as double points. is then the coefficient of the term containing .
For example, we can check that disappears on the knot 9_47 with its first five crossings taken as double points:
In[6]:=
V[Knot[9, 47], 4, {1, 2, 3, 4, 5}]
Out[6]=
V[Knot[9, 47], 4, {1, 2, 3, 4, 5}]
 The knot 9_47 with its first five crossings taken as double points.
The knot 9_47 with its first five crossings taken as double points.[Bar-Natan] ^ D. Bar-Natan, On the Vassiliev Knot Invariants, Topology 34 (1995) 423-472.
[BirmanLin] ^ J.S. Birman and X.-S. Lin, Knot Polynomials and Vassiliev's Invariants, Invent. Math. 111 (1993) 225-270.
Khovanov Homology
(See also: Tweaking JavaKh)
The Khovanov Homology of a knot or a link , also known as Khovanov's categorification of the Jones polynomial of , was defined by Khovanov in [Khovanov1] (also check [Bar-Natan1]), where the notation is closer to the notation used here). It is a graded homology theory; each homology group is in itself a direct sum of homogeneous components. Over a field one can form the two-variable "Poincaré polynomial" (which deserves the name "the Khovanov polynomial of "),
. (For In[1] see Setup)
In[2]:=
?Kh
Kh[L][q, t] returns the Poincare polynomial of the Khovanov Homology of a knot/link L (over a field of characteristic 0) in terms of the variables q and t. Kh[L, Program -> prog] uses the
program prog to perform the computation. The currently available programs are "FastKh", written in Mathematica by Dror Bar-Natan in the winter of 2005, "JavaKh-v1", written in java (java 1.5
required!) by Jeremy Green in the summer of 2005 and "JavaKh-v2" (default), an update of "JavaKh-v1" (now requiring java 1.6) written by Scott Morrison in 2008.
("JavaKh" is also available, currently an alias for "JavaKh-v2".)
The java programs are several thousand times faster than the Mathematica program, though java may not be available on some systems. "JavaKh2" also takes the option "Modulus -> p" which changes the characteristic of the ground field to p. If p==0 JavaKh works over the rational numbers; if p==Null JavaKh works over Z (see ?ZMod for the output format).
Thus for example, here's the Khovanov polynomial of the knot 5_1:
In[3]:=
kh = Kh[Knot[5, 1]][q, t]
Out[3]=
-5 -3 1 1 1 1
q + q + ------ + ------ + ------ + -----
15 5 11 4 11 3 7 2
q t q t q t q t
The Euler characteristic of the Khovanov Homology is (up to normalization) the Jones polynomial of . Precisely,
. Let us verify this in the case of 5_1:
In[4]:=
{kh /. t -> -1, Expand[(q+1/q)Jones[Knot[5, 1]][q^2]]}
Out[4]=
-15 -7 -5 -3 -15 -7 -5 -3
{-q + q + q + q , -q + q + q + q }

5_1
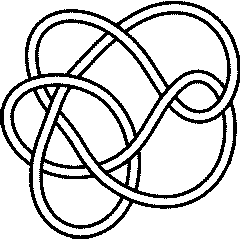
10_132
Khovanov's homology is a strictly stronger invariant than the Jones polynomial. Indeed, though :
In[5]:=
{
Jones[Knot[5, 1]] === Jones[Knot[10, 132]],
Kh[Knot[5, 1]] === Kh[Knot[10, 132]]
}
Out[5]=
{True, False}
The algorithm presently used by KnotTheory` is an efficient algorithm modeled on the Kauffman bracket algorithm of The Jones Polynomial, as explained in [Bar-Natan3] (which follows [Bar-Natan2]). Currently, two implementations of this algorithm are available:
- FastKh: My original implementation, written in Mathematica in the winter of 2005. This implementation can be explicitly invoked using the syntax
Kh[L, Program -> "FastKh"][q, t] or by changing the default behaviour of Kh by evaluating SetOptions[Kh, Program -> "FastKh"].
- JavaKh: In the summer of 2005 Jeremy Green re-implemented the algorithm in java (java 1.5 required, can be had from http://java.sun.com/) with much further care to the details, leading to an improvement factor of several thousands for large knots/links. This implementation is the default. It can also be explicitly invoked from within Mathematica using the syntax
Kh[L, Program -> "JavaKh"][q, t].
In[6]:=
Options[Kh]
Out[6]=
{ExpansionOrder -> Automatic, Program -> JavaKh-v2, Modulus -> 0,
KnotTheory`FastKh`Universal -> False, JavaOptions -> }
JavaKh takes an additional option, Modulus, which sets the characteristic of the ground field for the homology computations to or to a prime . Thus for example, the following four In lines imply that the Khovanov homology of the torus knot T(6,5) has both 3 torsion and 5 torsion, but no 7 torsion:
In[7]:=
T65 = TorusKnot[6, 5]; kh = Kh[T65][q, t];
In[8]:=
Kh[T65, Modulus -> 3][q, t] - kh
Out[8]=
43 13 43 14
q t + q t
In[9]:=
Kh[T65, Modulus -> 5][q, t] - kh
Out[9]=
35 10 35 11 39 11 39 12
q t + q t + q t + q t
In[10]:=
Kh[T65, Modulus -> 7][q, t] - kh
Out[10]=
0

T(6,5)
The following further example is a bit tougher. It takes my computer nearly an hour and some 256Mb of memory to find that the Khovanov homology of the 48-crossing torus knot T(8,7) has 3, 5 and 7 torsion but no 11 torsion:
In[11]:=
?JavaOptions
JavaOptions is an option to Kh. Kh[L, Program -> "JavaKh2", JavaOptions -> jopts] calls java with options jopts. Thus for example, JavaOptions -> "-Xmx256m" sets the maximum java heap size to 256MB - useful for large computations.
In[12]:=
SetOptions[Kh, JavaOptions -> "-Xmx256m"];
In[13]:=
T87 = TorusKnot[8, 7]; kh = Kh[T87][q, t];
In[14]:=
Factor[Kh[T87, Modulus -> 3][q, t] - kh]
Out[14]=
79 25
q t (1 + t)
In[15]:=
Factor[Kh[T87, Modulus -> 5][q, t] - kh]
Out[15]=
61 11 12 10 14 12 18 13
q t (1 + t) (1 + q t + q t + q t )
In[16]:=
Factor[Kh[T87, Modulus -> 7][q, t] - kh]
Out[16]=
61 14 8 6 12 7 10 8 14 9
q t (1 + t) (1 + q t + q t + q t + q t )
In[17]:=
Factor[Kh[T87, Modulus -> 11][q, t] - kh]
Out[17]=
0
JavaKh also works over the integers:
In[18]:=
?ZMod
ZMod[m] denotes the cyclic group Z/mZ. Thus if m=0 it is the infinite cyclic group Z and if m>0 it is the finite cyclic group with m elements. ZMod[m1, m2, ...] denotes the direct sum of ZMod[m1], ZMod[m2], ... .
For example, the 22nd homology group over of the torus knot T(8,7) at degree 73 is the 280 element torsion group :
In[19]:=
Coefficient[Kh[T87, Modulus -> Null][q, t], t^22 * q^73]
Out[19]=
ZMod[2, 4, 5, 7]
T(8,7) is currently not on the Knot Atlas. Let us see what it looks like:
In[20]:=
Show[TubePlot[TorusKnot[8, 7]]]
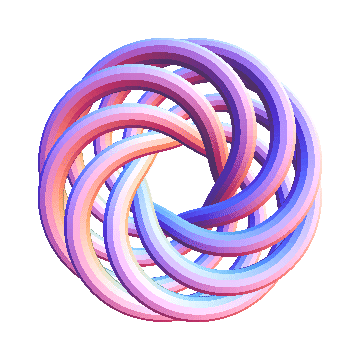
Out[20]=
-Graphics3D-
Finally, JavaKh may also be run outside of Mathematica, as the following example demonstrates:
drorbn@coxeter:.../KnotTheory: cd JavaKh
drorbn@coxeter:.../KnotTheory/JavaKh: java JavaKh
PD[X[3, 1, 4, 6], X[1, 5, 2, 4], X[5, 3, 6, 2]]
"+ q^1t^0 + q^3t^0 + q^5t^2 + q^9t^3 "
(Type java JavaKh -help for some further help).
(Warning, as of August 2008, you need to include the .jar files in JavaKh/jars on the classpath. If this causes confusion, ask Scott for a script that manages this automatically, or look at p. 29 of [2] for an example.)
Universal Khovanov homology, and reduced homology
The KnotTheory` package can now compute the universal homology over , the reduced homology over as well as directly computing the s-invariant. Type ?UniversalKh, ?KhReduced or ?sInvariant for more information.
The output of UniversalKh is a -linear combination of symbols KhE and KhC[n] for some positive integer .
The coefficients of these symbols are individually knot invariants, capturing all of the information in the spectral sequences (over ) for both unreduced and reduced homology.
The s-invariant can be extracted from the output of UniversalKh: the coefficient of KhE is exactly .
The usual 2-variable Khovanov polynomial Kh[K][q,t] can be recovered from UniversalKh[K][q,t] by using the substitution rules
{KhE->q+q^-1,KhC[1]->t^-1 q^-3+ q^1,KhC[n_]/;n>=2:>(q+q^-1)(t^-1 q^(-2n)+1)};
and similarly the reduced Khovanov polynomial KhReduced[K][q,t] is actually produced by substituting UniversalKh[K][q,t] using the rules
{KhE->q^-1,KhC[n_]:>t^-1 q^(-2n-1)+q^-1};
Unfortunately, much of the mathematics behind UniversalKh is not in print. There's some explanation in Scott's slides from Kyoto.
UniversalKh also takes the same JavaOptions option described above for Kh, which may be necessary to allow enough memory for large computations.
References
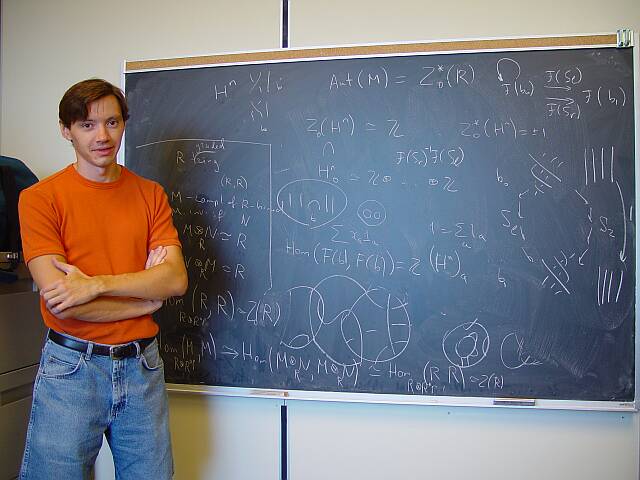 August 2002, Toronto: Mikhail Khovanov explaining his paper [Khovanov2].
August 2002, Toronto: Mikhail Khovanov explaining his paper [Khovanov2].[Bar-Natan1] ^ D. Bar-Natan, On Khovanov's categorification of the Jones polynomial, Algebraic and Geometric Topology 2-16 (2002) 337-370, arXiv:math.GT/0201043.
[Bar-Natan2] ^ D. Bar-Natan, Khovanov's Homology for Tangles and Cobordisms, Geometry and Topology 9-33 (2005) 1443-1499, arXiv:math.GT/0410495.
[Bar-Natan3] ^ D. Bar-Natan, I've Computed Kh(T(9,5)) and I'm Happy, talk given at Knots in Washington XX, George Washington University, February 2005.
[Khovanov1] ^ M. Khovanov, A categorification of the Jones polynomial, arXiv:math.QA/9908171.
[Khovanov2] ^ M. Khovanov, An invariant of tangle cobordisms, arXiv:math.QA/0207264.
See also A Khovanov homology bibliography.
Extras Included with KnotTheory`
The package KnotTheory` contains a few extras that are not directly related to knot theory.
Drawing with TubePlot
(For In[1] see Setup)
In[2]:=
?TubePlot
TubePlot[gamma, {t, t0, t1}, r, opts] plots the space curve gamma with the variable t running from t0 to t1, as a tube of radius r. The available options are TubeSubdivision, TubeFraming and TubePlotPrelude. All other options are passed on to Graphics3D. TubePlot[TorusKnot[m, n], opts] produces a tube plot of the (m,n) torus knot.
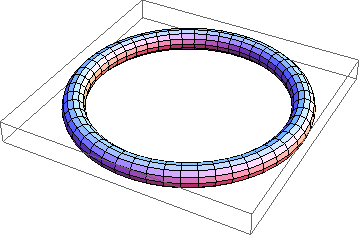
Thus here's a thin unknot:
In[3]:=
Show[TubePlot[{Cos[t], Sin[t], 0}, {t, 0, 2Pi}, 0.1]]
Out[3]=
-Graphics3D-
In[4]:=
?TubeSubdivision
TubeSubdivision is an option for TubePlot. TubePlot[__, TubeSubdivision -> {l, m} draws the tube subdivided to l pieces lengthwise and m pieces around. The default is TubeSubdivision -> {50, 12}.
In[5]:=
?TubeFraming
TubeFraming is an option for TubePlot. TubePlot[gamma, {t, __}, _, TubeFraming -> n] sets the framing of the tube (visible when TubeSubdivision -> {l, m} with small m) to be the vector n, which in itself may be a function of t. Thus TubeFraming -> {0,0,1} is "blackboard framing". TubeFraming -> Normal (default) uses the normal vector of the curve gamma.
In[6]:=
?TubePlotPrelude
TubePlotPrelude is an option for TubePlot. Its value is passed to Graphics3D before the main part of the plot, allowing to set various graphics options. For example, TubePlotPrelude -> EdgeForm[{}] will suppress the drawing of edges between the polygons making up the tube. The default is TubePlotPrelude -> {}.
Here's the same unknot, made thicker and not as smooth:
In[7]:=
Show[TubePlot[
{Cos[t], Sin[t], 0}, {t, 0, 2Pi}, 0.3, TubeSubdivision -> {6, 3}
]]
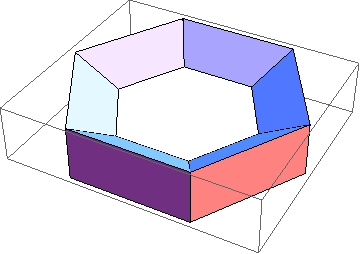
Out[7]=
-Graphics3D-
Let's play with the framing now:
In[8]:=
Show[TubePlot[
{Cos[t], Sin[t], 0}, {t, 0, 2Pi}, 0.2,
TubeSubdivision -> {50, 2},
TubeFraming -> {Cos[2t]Cos[t], Cos[2t]Sin[t], Sin[3t]}
]]
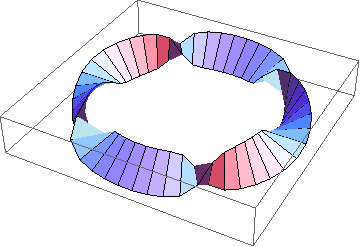
Out[8]=
-Graphics3D-
Here's an example that uses a prelude and passes options on to Graphics3D:
The last example serves as the basis for the definition of TubePlot[TorusKnot[m, n]]. Here's a final example:
In[10]:=
Show[TubePlot[TorusKnot[3, 5]]]
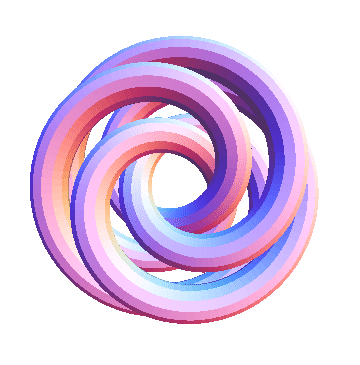
Out[10]=
-Graphics3D-
Standalone TubePlot
There may be some independent interest in the routine TubePlot, and hence it is available also as an independent package. Here it is: TubePlot.m (File:TubePlot.m).
WikiLink - The Mediawiki Interface
WikiLink is actually two separate things; firstly, a java class for interfacing with a mediawiki server, and secondly, a Mathematica package providing a wrapper around this. This page documents the Mathematica package, while the java class, and its addition functionality, will be documented elsewhere.
WikiLink is available as a standalone package, suitable for use with any Mediawiki installation, and is included in the KnotTheory` package.
License
WikiLink.nb, WikiLink.m and wikilink.jar are copyright Scott Morrison, available under your choice of the MIT, Apache or GPL licenses. The other components are copyright by other parties, all available under the Apache license.
Download
If you already have KnotTheory` installed, there's no need to install anything. The functionality of WikiLink is available as soon as you open KnotTheory`.
Otherwise, download WikiLink.zip. Unzip this anywhere you like. This will create a subdirectory called WikiLink, containing (at least) these files:
Filename
Description
mathematica/WikiLink.nb
The Mathematica notebook containing wrapper function definitions.
mathematica/WikiLink.m
The Mathematica package automatically generated from WikiLink.nb.
wikilink.jar
The WikiLink java classes and source code.
jars/jdom.jar
jars/commons-httpclient-3.0-rc2.jar
jars/commons-codec-1.3.jar
jars/commons-lang-2.1.jar
jars/commons-logging.jar
Libraries (all available under either GPL or the Apache license) required by wikilink.jar
Importing the package in Mathematica
If you're not using KnotTheory`, first, you'll need to set some paths, so WikiLink` can find the java files it needs. You need to add the "mathematica/" subdirectory of the WikiLink distribution to the Mathematica $Path.
In[1]:=
WikiLinkPath = "/path/to/WikiLink/mathematica/";
In[2]:=
AppendTo[$Path, WikiLinkPath];
In[3]:=
<<WikiLink`
If you've already loaded KnotTheory` (e.g., with the statement <<KnotTheory`), you can simply begin at this point.
We then try to connect to the wiki. Executing this line will prompt you for a username and password.
In[6]:=
CreateWikiConnection[
"http://katlas.math.toronto.edu/w/index.php",
InputString["Enter Your Username:"],
InputString["Enter Your Password:"]
]
The function WikiUserName[] checks that we're logged in
In[4]:=
?WikiUserName
WikiUserName[] returns either the name of the user you are logged in as, your IP address if you're not logged in, or $Failed if something more complicated has happened!
In[5]:=
WikiUserName[]
Out[5]=
ScottManualRobot
Usage
WikiLink` provides functions for checking your login status, getting and setting pages, as well as transparently extending some of Mathematica's string manipulation functions to wiki pages.
In[6]:=
?WikiUserName
WikiUserName[] returns either the name of the user you are logged in as, your IP address if you're not logged in, or $Failed if something more complicated has happened!
In[7]:=
?WikiGetPageText
WikiGetPageText[pagename] returns the raw text of the specified page.
In[8]:=
?WikiSetPageText
WikiSetPageText[pagename, text] overwrites the contents of the specificied page with the given text.
WikiSetPageText[pagename, text, summary] overwrites the contents of the specificied page with the given text and notes summary in the change log.
In[9]:=
?WikiSetPageTexts
WikiSetPageText[{{pagename1, text1},{pagename2,text2},...}] efficiently sets multiple pages, by first checking which texts are already up to date.
In[10]:=
?WikiUploadFile
WikiUploadFile[name, description] uploads the specified file to the wiki.
Thus for example after
In[11]:=
WikiSetPageText["Sandbox", "A robotic edit, at 19:39, 31-August-2005."]
Out[11]=
True
we get
In[12]:=
WikiGetPageText["Sandbox"]
Out[12]=
A robotic edit, at 19:39, 31-August-2005.
The function WikiSetPageTexts is most useful for batch uploads, as it does considerably more error checking, and filters out edits which won't change the page text. It takes as argument a list of {"title", "text"} pairs, and returns a list of those pairs which failed.
In[13]:=
WikiSetPageTexts[{{"Sandbox", "A robotic edit, by --~~"<>"~~"}, {"Sandbox2", "The determinant of the knot [[3_1]] is 3."}}]
Out[13]=
{}
In[14]:=
WikiGetPageText["Sandbox2"]
Out[14]=
The determinant of the knot [[3_1]] is 3.
String manipulation functions
WikiLink` provides functions WikiPageMatchQ, WikiPageFreeQ, WikiStringReplace and WikiStringCases. Each function works likes its usual Mathematica partner,
StringMatchQ,
StringFreeQ,
StringReplace
or StringCases. Instead of providing a string, or list of strings, as the first argument, you should give the name of a page, or a list of names.
You can use these to perform all sorts of editing tricks.
In[15]:=
WikiPageMatchQ[{"Sandbox", "Sandbox2"}, "determinant"]
Out[15]=
{False, False}
In[16]:=
WikiPageFreeQ[{"Sandbox", "Sandbox2"}, "[["~~(DigitCharacter..)~~"_"~~(DigitCharacter..)~~"]]"]
Out[16]=
{True, False}
In[17]:=
WikiStringCases[{"Sandbox", "Sandbox2"}, "[["~~ShortestMatch[__]~~"]]"]
Out[17]=
{{Sandbox, {[[User:ScottManualRobot|ScottManualRobot]]}},
{Sandbox2, {[[3_1]]}}}
In[18]:=
WikiStringReplace[{"Sandbox", "Sandbox2"}, "robotic edit"->"robotic edit (using WikiLink`)]
Out[18]=
$Failed
In[19]:=
WikiGetPageTexts[{"Sandbox", "Sandbox2"}]
Out[19]=
{{Sandbox, A robotic edit, by\
--[[User:ScottManualRobot|ScottManualRobot]] 14:54, 18 Feb 2006\
(EST)}, {Sandbox2, The determinant of the knot [[3_1]] is 3.}}
Troubleshooting
The instruction ShowJavaConsole[] will bring up a window in which some debugging information is displayed.
Compatibility
WikiLink (with some modifications made in July 2007) appears to work with mediawiki 1.10.1. Bug reports appreciated!
WikiLink has been tested against mediawiki 1.4.5beta3 and 1.4.7.
WikiLink has known issues on mediawiki 1.5.0. Retrieving multiple pages at once is broken. This appears to be a mediawiki bug, and will not be fixed. The same problem does not occur on mediawiki 1.5.8. --Scott 10:56, 27 Mar 2006 (EST)
I expect WikiGetPage text to continue working in mediawiki 1.5 and beyond, because it uses the stable interface Special:Export. Logging in and setting pages will quite likely break in the next version. If you've tried this, please let me know about your experiences. I'm hoping that soon (1.5?) Special:Import will become available, and I can switch to using this. --Scott 15:57, 31 Aug 2005 (EDT)
Todo
I'd love to create an Ant task which allows uploading a file to a wiki. We could then use this in build scripts for KnotTheory, etc. --Scott 04:07, 17 Sep 2005 (EDT)
See Also
All of the Mathematica notebooks in Category:Knot Atlas Maintenance Software rely on WikiLink, and so are good examples of how to use it.
You may also be interested in the Wikipedia page on mediawiki bots, and in particular the Python Wikipedia Robot Framework.
Lightly Documented Features
(For In[1] see Setup)
In[2]:=
?NumberOfKnots
NumberOfKnots[n] returns the number of knots with n crossings.
NumberOfKnots[n, Alternating|NonAlternating] returns the number of knots of the specified type.
In[3]:=
NumberOfKnots[16, NonAlternating]
Out[3]=
1008906
In[4]:=
?AlternatingQ
AlternatingQ[D] returns True iff the knot/link diagram D is alternating.
Among the knots with up to 11 crossings, 564 are alternating and 238 are not:
In[5]:=
Total[AlternatingQ /@ AllKnots[{0,11}]]
Out[5]=
238 False + 564 True
Further Knot Theory Software
KnotPlot
Many of the images appearing in The Knot Atlas were created using Rob Scharein's program KnotPlot:
Knotscape
Many of the images appearing in The Knot Atlas were created using Jim Hoste's and Morwen Thistlethwaite's program Knotscape.
Xknots
Xknots, developed by Javier Rodríguez is a program that produces postscript knot images.
How to Edit this Manual...
To a large extent, editing this manual is easy --- just as easy as editing a page at Wikipedia, or any other wiki. There's some good help on that available at Wikipedia:How to edit a page. However, because we also use Mathematica code within the manual, and automatically generate the output, there are a few things you need to be aware of. Read on! (or don't -- just go edit!)
The Basic Rules
Knot Atlas manual pages are editable and are edited by both humans and robots (dedicated computer programs). Both sides have to be careful not to step into each other's territory. Under the current treaties, robots are responsible for simulated Mathematica output and for certain numerical values that are computed by KnotTheory`. Their territory always lies between <!--$ and <!--END--> tags. Humans are responsible for everything else, including brief ventures into the robot's territories to tell the robots what to do.
Human Edits
To perform a human edit, simply click on the "edit" link at the top of any manual page (or indeed, at the top of almost any other wiki page) and begin editing, saving your work at the end. Be careful not to modify anything in the robots' territory, delimited by <!--$ and <!--END--> tags.
You may find the Local Clip Art library useful, or this brief description of math mode.
If you're adding a new manual page, start it with "{{Manual TOC Sidebar}}" (this produces the table of contents (TOC) sidebar on the right) and make sure to add your page to the table of contents at Manual Table of Contents and to the Printable Manual list-of-sections.
If you are only interested in an edit confined to a human territory, you don't need to read any further.
What Robots Do
Before a human can tell a robot what to do, (s)he must understand the simple way in which robots work. Robots do just one simple thing, and only when instructed to it. Here's how they work:
- They search the text of a manual page for patterns of the form <!--$robot instructions$-->old robotic response<!--END-->.
- They study the robot instructions and compute something.
- They print the output, i.e. the new robotic response, in place of the old robotic response. Just to be sure that humans don't modify the new robotic response, robots precede it with a short human do not enter phrase. Dror's robot's favourite is Robot Land, no human edits to "END".
- Robots never modify their own instructions or venture to human territories.
Human Ventures into Robot Lands
It is not a good idea for a human to modify a robotic response, as these changes will be overwritten the next time a robot roams the page. (On the other hand, it doesn't break anything in the meantime.) Better, humans can control the robots.
- To create a new robot territory, put the pattern <!--$robot instructions$--><!--END--> in the desired place. Note: You must put in <!--END--> by hand! The next time a robot visits it will follow the instructions and place its response between the $--> and <!--END--> tags.
- To remove an existing robot territory, simply remove everything from the <!--$ tag to the <!--END-->.
- To modify an existing robot territory, change the content of the robot instructions, between the <!--$ tag and the $--> tag. The next time a robot visits it will follow the new instructions.
Giving Robots Instructions
Currently robots understand the following kinds of instructions:
<!--$instructions$-->
Description
Example
Formatted Output
<!--$$<< KnotTheory`$$-->
Simulate In[1] of a KnotTheory` session.
<!--$$<< KnotTheory`$$--> <!--END-->
In[2]:= << KnotTheory`
Loading KnotTheory` version of March 22, 2011, 21:10:4.67737.
Read more at http://katlas.org/wiki/KnotTheory.
<!--$$Input line$$-->
Simulate a Mathematica "In Out" pair.
<!--$$Jones[Knot[3, 1]][q]$$--> <!--END-->
In[3]:=
Jones[Knot[3, 1]][q]
Out[3]=
-4 -3 1
-q + q + -
q
(if output is Null)
<!--$$Jones[Knot[4, 1]][q];$$--> <!--END-->
In[4]:=
Jones[Knot[4, 1]][q];
(if graphics)
<!--$$Show[DrawPD[Knot[5, 1]]]$$--> <!--END-->
In[5]:=
Show[DrawPD[Knot[5, 1]]]
Out[5]=
-Graphics-
<!--$$?Symbol$$-->
Simulate a Mathematica help line.
<!--$?Jones$--> <!--END-->
In[6]:=
?Jones
Jones[L][q] computes the Jones polynomial of a knot or link L as a function of the variable q.
(if Symbol::about exists)
<!--$$?Kauffman$$--> <!--END-->
In[7]:=
?Kauffman
Kauffman[K][a, z] computes the Kauffman polynomial of a knot or link K, in the variables a and z.
In[8]:=
Kauffman::about
The Kauffman polynomial program was written by Scott Morrison.
<!--$inlined command$-->
Perform a Mathematica command "in line".
There are <!--$NumberOfKnots[10]$--> <!--END--> knots with 10 crossings.
There are 165 knots with 10 crossings.
Calling for Robotic Action
Copy Dror's robot ManualSpliceRobot.nb (File:ManualSpliceRobot.nb) to your own computer (it is now yours). The robot is a Mathematica notesbook; simply open it and follow the instructions within. You must have the package KnotTheory` around, Scott's Mathematica WikiLink package and java (which comes bundled with Mathematica 4.2 and up). You will need to specify a few paths and your (or better, your robot's) Username and Password on the Knot Atlas wiki. Good luck!
Teaching Robots New Tricks
At the moment robots do not ignore their instructions even if they don't understand them, so there can be only one robot master teaching robots what to do, or else chaos may ensue. If you want to build a better robot or extend Dror's, do it in your sandbox but don't let it roam on public pages. When the new or extended robot is fully trained, and provided its actions extends Dror's robot, send it to Dror and he will upgrade his robot and make the new robot public.
About this Manual...
Bibliography

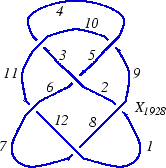















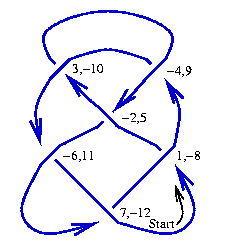




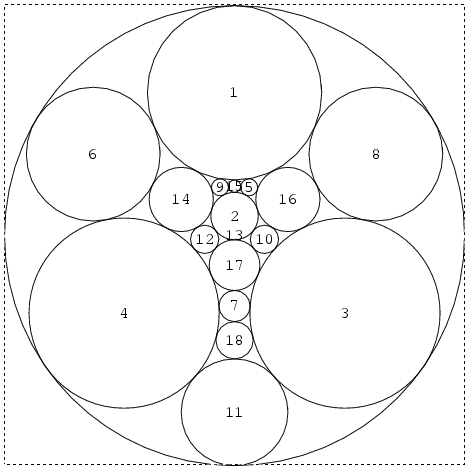
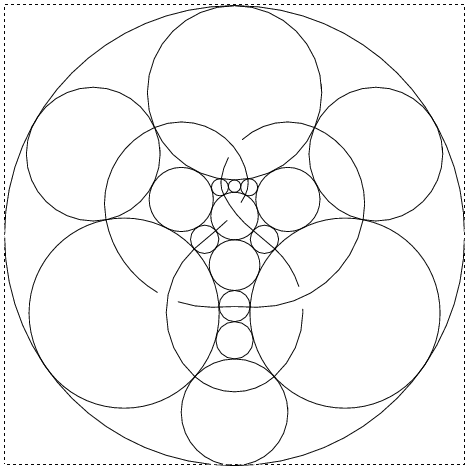













![{\displaystyle {\mathbb {Z} }[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97a786720fa81d7d0cf7400c3ff3f72e892fbc33)


































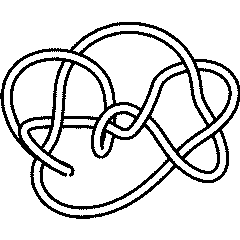



















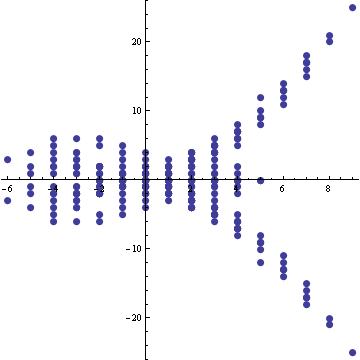





























![{\displaystyle \mathbb {N} [q,t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/acbaffd1db67f47e1ca5f6c63bed36cff66b7673)